"The reliability of any set of measurements is logically defined as the proportion of their variance that is true variance... We think of the total variance of a set of measures as being made up of two sources of variance: true variance and error variance... The true measure is assumed to be the genuine value of whatever is being measured... The error components occur independently and at random" (Guilford 1965, p.439-40).
Observed Variance = "True" Variance + Error Variance
Reliability = "True" Variance / Observed Variance
In Rasch terms, "True" valiance is the "adjusted" variance (observed variance adjusted for measurement error). Error Variance is a mean-square error (derived from the model) inflated by misfit to the model encountered in the data.
Kubiszyn and Borich (1993, p.353) say "an acceptable standardized test should have reliability coefficients of about .95 for internal consistency". But "reliability depends upon the population measured as well as the measuring instrument... One should speak of the reliability of a certain instrument applied to a certain population under certain conditions" (Guilford p.439). This is because the "true" variance is a characteristic of the sample tested and the "error" variance is a characteristic of the measuring instrument.
Since reliability is restricted to the range 0 to 1, it is convenient to express it as a separation coefficient with range 0 to infinity:
G = Separation = sqrt(Rel./(1-Rel.)) =
"True" Standard Deviation / Error Standard Deviation
In Rasch literature, the "True" S.D. is often called the "Adjusted" (for measurement error) S.D.
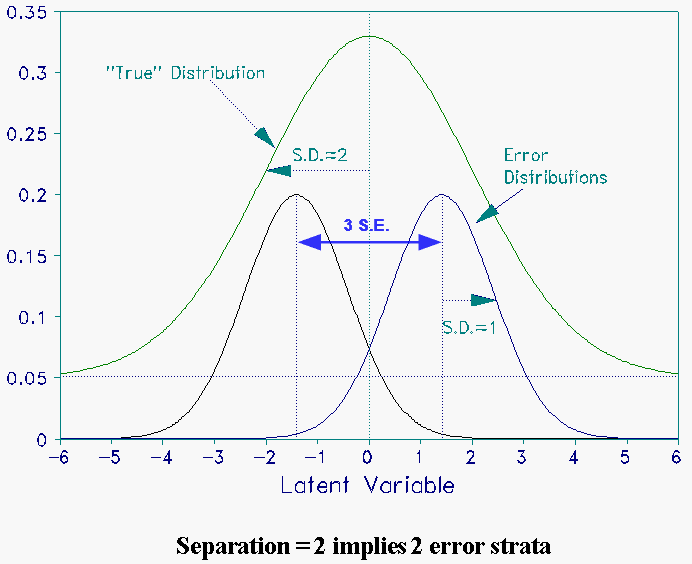
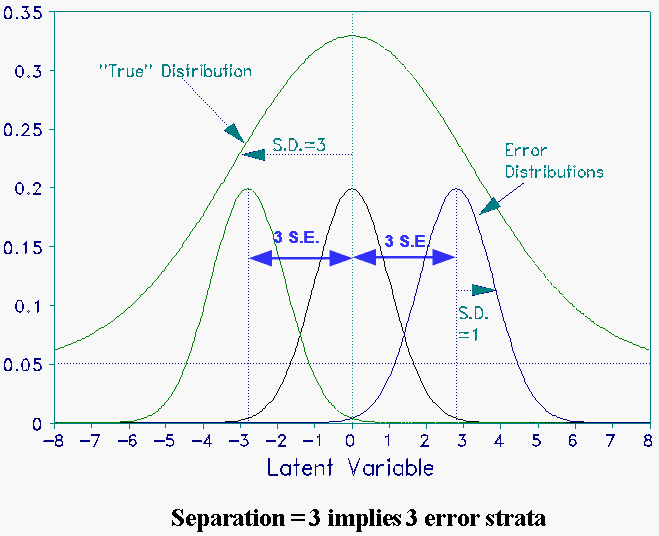
Separation is the number of statistically different performance strata that the test can identify in the sample. This can be pictured by placing an error distribution in each stratum (see Examples). A separation of "2" implies that only two levels of performance can be consistently identified by the test for samples like the one tested. Kubiszyn & Borich's 0.95 corresponds to a separation of 4.5, i.e., 4 consistently identifiable strata. (See RMT 6:3 p. 238 for a Table of Reliability - Separation equivalences). Compare the Separation plot with with a different definition of "ability strata" at Number of Person or Item Strata (4G+1)/3 (RMT 16:3).
Example 1: Separation = 2.0, "True" S.D. = 2.0, Error S.D. = 1.0
Reliability = (2.0*2.0) / (2.0*2.0 + 1.0*.1.0) = 0.8

Example 2:Separation = 3.0, "True" S.D. = 3.0, Error S.D. = 1.0
Reliability = (3.0*3.0) / (3.0*3.0 + 1.0*.1.0) = 0.9
In the graph below, notice that the middle error strata is from -1.5 Error S.D. to +1.5 Error S.D.
Guilford J. P. (1965) Fundamental Statistics in Psychology and Education. 4th Edn. New York: McGraw-Hill.
Kubiszyn T., Borich G. (1993) Educational Testing and Measurement. New York: Harper Collins.
Note:
The levels in the observed distribution are 3*"Observed S.D."/G apart, centered on the sample mean.
Reliability and separation. Wright BD. … Rasch Measurement Transactions, 1996, 9:4 p.472
| Forum | Rasch Measurement Forum to discuss any Rasch-related topic |
Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement
Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.
| Coming Rasch-related Events | |
|---|---|
| Apr. 21 - 22, 2025, Mon.-Tue. | International Objective Measurement Workshop (IOMW) - Boulder, CO, www.iomw.net |
| Jan. 17 - Feb. 21, 2025, Fri.-Fri. | On-line workshop: Rasch Measurement - Core Topics (E. Smith, Winsteps), www.statistics.com |
| Feb. - June, 2025 | On-line course: Introduction to Classical Test and Rasch Measurement Theories (D. Andrich, I. Marais, RUMM2030), University of Western Australia |
| Feb. - June, 2025 | On-line course: Advanced Course in Rasch Measurement Theory (D. Andrich, I. Marais, RUMM2030), University of Western Australia |
| May 16 - June 20, 2025, Fri.-Fri. | On-line workshop: Rasch Measurement - Core Topics (E. Smith, Winsteps), www.statistics.com |
| June 20 - July 18, 2025, Fri.-Fri. | On-line workshop: Rasch Measurement - Further Topics (E. Smith, Facets), www.statistics.com |
| Oct. 3 - Nov. 7, 2025, Fri.-Fri. | On-line workshop: Rasch Measurement - Core Topics (E. Smith, Winsteps), www.statistics.com |
The URL of this page is www.rasch.org/rmt/rmt94n.htm
Website: www.rasch.org/rmt/contents.htm