Predicting Reliabilities and Separations of Different Length Tests

The Spearman-Brown "prophecy" formula predicts test (sample) reliabilities for similar dichotomous tests of different lengths. When the sample reliability of a hypothetical test of M items is to be predicted from a similar test of K items:


or, in terms of the sample Wright's Separation index:


Note: in RUMM2020 documentation, the "Separation Index" is the Rasch reliability (R). Wright' Separation = √ ((R)/(1-R))

Thus, the sample Separation index for a "unit" test of 1 item is SepK/K, and its sample reliability is RK/(1+K(1-RK)). These formulae also hold for tests containing homogeneous polytomous items, and for the estimation of item reliability and separation indices.

Here is an extension for the sample reliability of a test of polytomous items with differing numbers of categories.

A polytomous item of m ordered categories contains m-1 dichotomous category boundaries. The number of items in the known test is K. Then the number of active categories in the known test is:


where mi is the number of categories for item i (no matter how it is modeled). Thus a test of K items contains CK - K dichotomous decisions.

Then, for a similar test of M items, its sample reliability RM is:


and its sample Separation index, SepM, is:


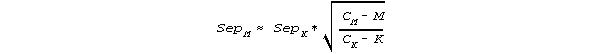
and the Separation index for a "unit" test comprising 1 category boundary is

SepK/(CK-K),

and its reliability is

RK/(1+(CK-K)(1-RK)).

John Michael Linacre

  1. Reliability, separation, strata statistics, Fisher WP Jr. … 6:3 p.238
  2. Reliability and separation nomograms, Linacre JM. … 1995, 9:2 p.421
  3. Reliability and separation, Wright BD. … 1996, 9:4 p.472
  4. Predicting Reliabilities and Separations of Different Length Tests, Linacre, J.M. … 2000, 14:3 p.767
  5. Going beyond Unreliable Reliabilities, Mallinson T., Stelmack J. … 2001, 14:4 p.787-8
  6. Separation, Reliability and Skewed Distributions: Statistically Different Levels of Performance, Wright B.D. … 2001, 14:4 p.786
  7. Number of Person or Item Strata (4G+1)/3, Wright BD, Masters GN. … 2002, 16:3 p.888
  8. Cash value of Reliability, WP Fisher … Rasch Measurement Transactions, 2008, 22:1 p. 1160

Predicting Reliabilities and Separations of Different Length Tests. Linacre, J.M. … Rasch Measurement Transactions, 2000, 14:3 p.767



Rasch Books and Publications
Invariant Measurement: Using Rasch Models in the Social, Behavioral, and Health Sciences, 2nd Edn. George Engelhard, Jr. & Jue Wang Applying the Rasch Model (Winsteps, Facets) 4th Ed., Bond, Yan, Heene Advances in Rasch Analyses in the Human Sciences (Winsteps, Facets) 1st Ed., Boone, Staver Advances in Applications of Rasch Measurement in Science Education, X. Liu & W. J. Boone Rasch Analysis in the Human Sciences (Winsteps) Boone, Staver, Yale
Introduction to Many-Facet Rasch Measurement (Facets), Thomas Eckes Statistical Analyses for Language Testers (Facets), Rita Green Invariant Measurement with Raters and Rating Scales: Rasch Models for Rater-Mediated Assessments (Facets), George Engelhard, Jr. & Stefanie Wind Aplicação do Modelo de Rasch (Português), de Bond, Trevor G., Fox, Christine M Appliquer le modèle de Rasch: Défis et pistes de solution (Winsteps) E. Dionne, S. Béland
Exploring Rating Scale Functioning for Survey Research (R, Facets), Stefanie Wind Rasch Measurement: Applications, Khine Winsteps Tutorials - free
Facets Tutorials - free		 Many-Facet Rasch Measurement (Facets) - free, J.M. Linacre Fairness, Justice and Language Assessment (Winsteps, Facets), McNamara, Knoch, Fan
Other Rasch-Related Resources: Rasch Measurement YouTube Channel
Rasch Measurement Transactions & Rasch Measurement research papers - free An Introduction to the Rasch Model with Examples in R (eRm, etc.), Debelak, Strobl, Zeigenfuse Rasch Measurement Theory Analysis in R, Wind, Hua Applying the Rasch Model in Social Sciences Using R, Lamprianou El modelo métrico de Rasch: Fundamentación, implementación e interpretación de la medida en ciencias sociales (Spanish Edition), Manuel González-Montesinos M.
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch Rasch Models for Measurement, David Andrich Constructing Measures, Mark Wilson Best Test Design - free, Wright & Stone
Rating Scale Analysis - free, Wright & Masters
Virtual Standard Setting: Setting Cut Scores, Charalambos Kollias Diseño de Mejores Pruebas - free, Spanish Best Test Design A Course in Rasch Measurement Theory, Andrich, Marais Rasch Models in Health, Christensen, Kreiner, Mesba Multivariate and Mixture Distribution Rasch Models, von Davier, Carstensen

To be emailed about new material on www.rasch.org
please enter your email address here:

I want to Subscribe: & click below
I want to Unsubscribe: & click below

Please set your SPAM filter to accept emails from Rasch.org

Rasch Measurement Transactions welcomes your comments:

Your email address (if you want us to reply):

If Rasch.org does not reply, please post your message on the Rasch Forum
 

ForumRasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

Coming Rasch-related Events
Apr. 21 - 22, 2025, Mon.-Tue. International Objective Measurement Workshop (IOMW) - Boulder, CO, www.iomw.net
Jan. 17 - Feb. 21, 2025, Fri.-Fri. On-line workshop: Rasch Measurement - Core Topics (E. Smith, Winsteps), www.statistics.com
Feb. - June, 2025 On-line course: Introduction to Classical Test and Rasch Measurement Theories (D. Andrich, I. Marais, RUMM2030), University of Western Australia
Feb. - June, 2025 On-line course: Advanced Course in Rasch Measurement Theory (D. Andrich, I. Marais, RUMM2030), University of Western Australia
May 16 - June 20, 2025, Fri.-Fri. On-line workshop: Rasch Measurement - Core Topics (E. Smith, Winsteps), www.statistics.com
June 20 - July 18, 2025, Fri.-Fri. On-line workshop: Rasch Measurement - Further Topics (E. Smith, Facets), www.statistics.com
Oct. 3 - Nov. 7, 2025, Fri.-Fri. On-line workshop: Rasch Measurement - Core Topics (E. Smith, Winsteps), www.statistics.com

 

The URL of this page is www.rasch.org/rmt/rmt143j.htm

Website: www.rasch.org/rmt/contents.htm