The Expected Value of a Point-Biserial (or Similar) Correlation

Interpreting the observed value of a point-biserial correlation is made easier if we can compare the observed value with its expected value. Is the observed value much higher than the expected value (indicating dependency in the data) or much lower than expected (indicating unmodeled noise)? With knowledge of how the observed value compares with its expected value, there is no need for arbitrary rules such as "Delete items with point-biserials less than 0.2."

The general formula for a Pearson correlation coefficient is:

(1)

Point-Biserial Correlation (including all observations in the correlated raw score)

Suppose that Xn is Xni the observation of person n on item i. Yn is Rn, the raw score of person n, then the point-biserial correlation is:

(2)

where X. is the mean of the {Xni} for item i, and R. is the mean of the Rn.

According to the Rasch model, the expected value of Xni is Eni and the model variance of Xni around its expectation is Wni. The model variances of X.i, Rn, R. are ignored here. S(Eni) = S(Xni), so that E.i = X.i.

Thus an estimate of the expected value of the point-measure correlation is given by the Rasch model proposition that: Xni = Eni±√Wni

(3)

Since ±√Wni is a random residual, its cross-product with any other variable is modeled to be zero. Thus

(4)

which provides a convenient formula for computing the expected value of the point-biserial correlation. Also see Note below

Point-Biserial Correlation (excluding current observation from the correlated raw score)

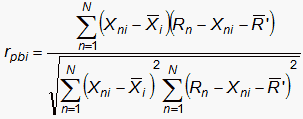
(5)

where R.'is the mean of the R_n-X_ni.

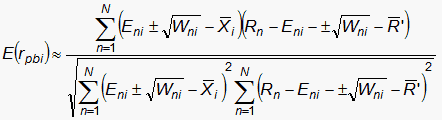
(6)

(7)

is the expected value of the point-biserial correlation excluding the current observation.

Point-Measure Correlation

Similarly, suppose that Yn is Bn, the ability measure of person n, then the point-measure correlation is:

(8)

where B. is the mean of the Bn.

Thus an estimate of the expected value of the point-measure correlation is:

(9)

which provides a convenient formula for computing the expected value of a point-measure correlation.

John Michael Linacre

Here is a worked example for a point-measure correlation:

Later note: Experience suggests that W_ni*(N-2)/N is a better term in the divisors than W_ni, so that the expected correlation for 2 observations becomes its observed value of ±1.0. The "expected value" derivation is asymptotic for large N. When we have only small N, in particular only two points, the derivation degrades. The correction of (N-2)/N makes the expected value more reasonable especially in the boundary condition of only two points. When there are only two points, (N-2) makes the W_ni term disappear, so that the expected value of the correlation becomes +1.0 or -1.0 (or undefined), which will generally match its empirical value.

The Expected Value of a Point-Biserial (or Similar) Correlation. Linacre J.M. … Rasch Measurement Transactions, 2008, 22:1 p. 1154

Rasch-Related Resources: Rasch Measurement YouTube Channel
Rasch Measurement Transactions & Rasch Measurement research papers - free	An Introduction to the Rasch Model with Examples in R (eRm, etc.), Debelak, Strobl, Zeigenfuse	Rasch Measurement Theory Analysis in R, Wind, Hua	Applying the Rasch Model in Social Sciences Using R, Lamprianou	El modelo métrico de Rasch: Fundamentación, implementación e interpretación de la medida en ciencias sociales (Spanish Edition), Manuel González-Montesinos M.
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Rasch Models for Measurement, David Andrich	Constructing Measures, Mark Wilson	Best Test Design - free, Wright & Stone Rating Scale Analysis - free, Wright & Masters
Virtual Standard Setting: Setting Cut Scores, Charalambos Kollias	Diseño de Mejores Pruebas - free, Spanish Best Test Design	A Course in Rasch Measurement Theory, Andrich, Marais	Rasch Models in Health, Christensen, Kreiner, Mesba	Multivariate and Mixture Distribution Rasch Models, von Davier, Carstensen
Rasch Books and Publications: Winsteps and Facets
Applying the Rasch Model (Winsteps, Facets) 4th Ed., Bond, Yan, Heene	Advances in Rasch Analyses in the Human Sciences (Winsteps, Facets) 1st Ed., Boone, Staver	Advances in Applications of Rasch Measurement in Science Education, X. Liu & W. J. Boone	Rasch Analysis in the Human Sciences (Winsteps) Boone, Staver, Yale	Appliquer le modèle de Rasch: Défis et pistes de solution (Winsteps) E. Dionne, S. Béland
Introduction to Many-Facet Rasch Measurement (Facets), Thomas Eckes	Rasch Models for Solving Measurement Problems (Facets), George Engelhard, Jr. & Jue Wang	Statistical Analyses for Language Testers (Facets), Rita Green	Invariant Measurement with Raters and Rating Scales: Rasch Models for Rater-Mediated Assessments (Facets), George Engelhard, Jr. & Stefanie Wind	Aplicação do Modelo de Rasch (Português), de Bond, Trevor G., Fox, Christine M
Exploring Rating Scale Functioning for Survey Research (R, Facets), Stefanie Wind	Rasch Measurement: Applications, Khine	Winsteps Tutorials - free Facets Tutorials - free	Many-Facet Rasch Measurement (Facets) - free, J.M. Linacre	Fairness, Justice and Language Assessment (Winsteps, Facets), McNamara, Knoch, Fan

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt221e.htm

Website: www.rasch.org/rmt/contents.htm