An Adjustment for Sample Size in DIF Analysis

A statistical test for differential item functioning (DIF, item bias) between two groups, 1 and 2, is:

[1]

where di(1) - di(2) is the shift of the item i measures between groups 1 and 2; sei(1) and sei(2) are the standard errors of the item measures. A shift greater than 0.5 logits is considered evidence of DIF, and a t value of 1.96 or more is statistically significant (p<.05) for large samples (Draba, 1977). The ETS DIF Classification is similar, but more elaborate. Draba's rule approximates the ETS Category B rule.

Formula [1] has been employed in a 21 items test, answered by 21820 persons, and the purpose is to detect gender bias. Standard errors are deliberately shown with 4 decimal places. It appears that even for small shift values, 20 of the 21 items produce significant ti(12) values, indicating that practically all the items show gender bias according to the significance rule alone. The same analysis was developed with sub-samples of 250 women and 250 men, now only 5 of the 21 items produce significant t values and so it is a minority of items that show gender bias. The main reason of the difference in results is that the standard errors of the item measures depend on the sizes of the focus and reference groups. But, according to Clauser & Hambleton (1994), "DIF analysis should be based on the largest sample available", so their guideline implies that even the smallest difference could be significant, nullifying the ETS Significance rule.

It can be seen that the conventional t values, ti(12), differ considerably across calculations. The measure estimates for the large sample are more precise than for the sub-sample, so the large sample produces smaller standard errors of measurement and higher t values. This suggests that a DIF Significance test is needed that is robust against sample size. Here is one based on computationally normalizing the empirical sample size of N to a standard sample size of 100:

[2]

The reference value of 100 has been chosen because it is not only a simple number to remember, but also because the mean S.E.normalized for item p-values between 0.001 and 0.999 is 0.965, i.e., close to 1, and, as can be seen in Fig. 1, the minimum possible value of S.E.normalized is 0.2. These values are of the same order of magnitude as the t values expected according to formula [1]. In addition, t values bigger than 1.96 may occur for shifts of 0.55 (Fig. 2), which closely corresponds to the half logit rule, so the conclusions of the DIF size and DIF significance rules are in accord. For a closer match with the ETS criteria for DIF Category B, instead of 100, normalize with 100*(0.43/0.55)^2 ≈ 60.

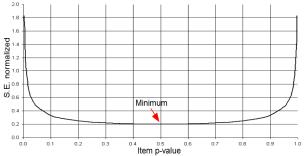
Figure 1. Values of S.E.normalized for different item p-values.

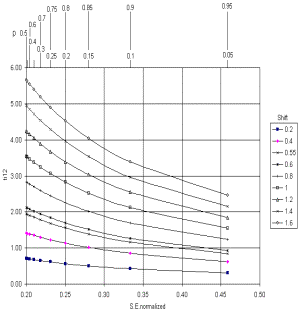
Figure 2. Theoretical t values as a function of shift and S.E. normalized

Figure 2 shows that, independently of the S.E., shifts below 0.55 imply that no item bias will be present and that shifts above 1.3 imply item bias (both are close to the 0.5 logit rule and the 1.5 logit rule). Therefore bias depends on S.E.normalized (i.e., item-sample targeting) only for shifts between 0.55 and 1.3 logits.

The right-hand columns of Table 1 show the normalized standard errors and t-tests. It can be seen that the size of S.E.normalized is comparable between the complete sample and the sub-sample and that the t values, ti(12)n, are similar. The DIF sizes and significances are now in closer accord. It can now be seen that is it meaningful to apply both the size and significance criteria in classifying items for DIF.

Agustín Tristán

Clauser B.E. & Hambleton, R.K. (1994) Review of Differential Item Functioning, P. W. Holland, H. Wainer. Journal of Educational Measurement, 31, 1, 88-92.

Draba R.E. (1977) The identification and interpretation of item bias. Educational Statistics Laboratory. Memo 25. University of Chicago. www.rasch.org/memo25.htm

See also RMT 1989 3:2 51-53

An Adjustment for Sample Size in DIF Analysis, Tristan A. … Rasch Measurement Transactions, 2006, 20:3 p. 1070-1

Rasch-Related Resources: Rasch Measurement YouTube Channel
Rasch Measurement Transactions & Rasch Measurement research papers - free	An Introduction to the Rasch Model with Examples in R (eRm, etc.), Debelak, Strobl, Zeigenfuse	Rasch Measurement Theory Analysis in R, Wind, Hua	Applying the Rasch Model in Social Sciences Using R, Lamprianou	El modelo métrico de Rasch: Fundamentación, implementación e interpretación de la medida en ciencias sociales (Spanish Edition), Manuel González-Montesinos M.
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Rasch Models for Measurement, David Andrich	Constructing Measures, Mark Wilson	Best Test Design - free, Wright & Stone Rating Scale Analysis - free, Wright & Masters
Virtual Standard Setting: Setting Cut Scores, Charalambos Kollias	Diseño de Mejores Pruebas - free, Spanish Best Test Design	A Course in Rasch Measurement Theory, Andrich, Marais	Rasch Models in Health, Christensen, Kreiner, Mesba	Multivariate and Mixture Distribution Rasch Models, von Davier, Carstensen
Rasch Books and Publications: Winsteps and Facets
Applying the Rasch Model (Winsteps, Facets) 4th Ed., Bond, Yan, Heene	Advances in Rasch Analyses in the Human Sciences (Winsteps, Facets) 1st Ed., Boone, Staver	Advances in Applications of Rasch Measurement in Science Education, X. Liu & W. J. Boone	Rasch Analysis in the Human Sciences (Winsteps) Boone, Staver, Yale	Appliquer le modèle de Rasch: Défis et pistes de solution (Winsteps) E. Dionne, S. Béland
Introduction to Many-Facet Rasch Measurement (Facets), Thomas Eckes	Rasch Models for Solving Measurement Problems (Facets), George Engelhard, Jr. & Jue Wang	Statistical Analyses for Language Testers (Facets), Rita Green	Invariant Measurement with Raters and Rating Scales: Rasch Models for Rater-Mediated Assessments (Facets), George Engelhard, Jr. & Stefanie Wind	Aplicação do Modelo de Rasch (Português), de Bond, Trevor G., Fox, Christine M
Exploring Rating Scale Functioning for Survey Research (R, Facets), Stefanie Wind	Rasch Measurement: Applications, Khine	Winsteps Tutorials - free Facets Tutorials - free	Many-Facet Rasch Measurement (Facets) - free, J.M. Linacre	Fairness, Justice and Language Assessment (Winsteps, Facets), McNamara, Knoch, Fan

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt203e.htm

Website: www.rasch.org/rmt/contents.htm