Pass Rates: Reporting in a Stable Context

Every new test form differs in difficulty from every previous form. Every computer-adaptive (CAT) test has its own difficulty. The communication of individual test results must overcome this hurdle. Every group of test respondents has its own ability distribution. The communication of group performance must overcome this further hurdle. On many high-stakes tests, the perception of fairness hinges on how these challenges are met.

The National Certification Corporation for the Obstetric, Gynecologic and Neonatal Nursing Specialties (NCC) faces the recurring problem of developing new test forms semi-annually, establishing criterion pass-fail levels on those forms, administering them to new examinee populations, and then reporting an equitable pass. In practice, it was observed that the actual pass rate varied across forms. But it was not clear whether this was due only to changes in examinee ability distribution.

A determined, and ultimately successful, quest was undertaken to discover a process that produces a stable, defensible pass rate. The quality of the test items themselves had already been scrutinized closely, so the first focus was on the establishment of a stable pass-fail point despite the inevitable changes in test difficulty and examinee ability. The raw-score pass-point selection methods of Nedelsky, Angoff, Ebel and Jaeger were attempted, as well as the 1986 Wright-Grosse Rasch-based method (RMT 7:3 315-316). The best of the raw-score methods for producing a stable pass-rate was seen to be the "modified" Angoff approach, but far better was Wright-Grosse (see my 1995 AERA paper, "Objective Standard Setting"). [Another attempt at objective standard setting is the Lewis, Mitzel, Green (1996) Bookmark standard-setting procedure.]

The second focus was on the problem of differing test difficulties. NCC's solution is similar to that recommended by Stocking (1994). Equate the actual test (in Stocking's case, each examinee's CAT test) to a "standard" test using conventional Rasch equating technology. Report the results in terms of that "standard" test. This accounts for variation in test difficulty. Equating the administered test to a "standard" test also enables the newly set pass-fail point to be compared to the pass-fail points set for any previously equated tests.

The third focus was on the varying person ability distributions. The actual pass rate must go up when the group is more able, down when it is less able. Decisions by an examination board that 75% will pass every time (regardless of test difficulty or examinee abilities) lead to obvious unfairness and to test-wise strategies as to when to take the test. But reporting different success rates from test to test gives the impression that the pass-fail point is haphazard. The solution was to report the pass rate that would have been achieved by examinees with a "standard" ability distribution who were imagined to take the "standard" test into which the newly set pass-fail point had been equated. The percent of "standard" examinees above this equated pass-fail point is the stable pass rate.

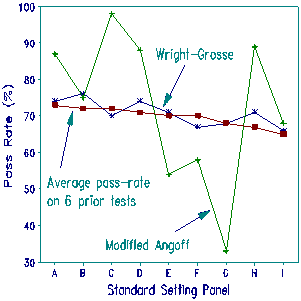
The Plot compares the pass-rates observed for one test administration based on modified Angoff (the best of all raw score methods) and Wright-Grosse, reported in terms of a standard test and a standard examinee distribution. Also shown are the empirical pass-rates (averaged over the previous 6 years) for each of 9 standard setting panels. Only the Wright-Grosse method produces the stable results that NCC was seeking.

Stocking ML (1994) An alternative method for scoring adaptive tests. Research report RR-94-48. Princeton NJ: ETS.

Pass rates: Reporting in a stable context. Stone GE. … Rasch Measurement Transactions, 1995, 9:1 p.417

Rasch Publications
Rasch Measurement Transactions (free, online)	Rasch Measurement research papers (free, online)	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Applying the Rasch Model 3rd. Ed., Bond & Fox	Best Test Design, Wright & Stone
Rating Scale Analysis, Wright & Masters	Introduction to Rasch Measurement, E. Smith & R. Smith	Introduction to Many-Facet Rasch Measurement, Thomas Eckes	Invariant Measurement: Using Rasch Models in the Social, Behavioral, and Health Sciences, George Engelhard, Jr.	Statistical Analyses for Language Testers, Rita Green
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Journal of Applied Measurement	Rasch models for measurement, David Andrich	Constructing Measures, Mark Wilson	Rasch Analysis in the Human Sciences, Boone, Stave, Yale
in Spanish:	Análisis de Rasch para todos, Agustín Tristán		Mediciones, Posicionamientos y Diagnósticos Competitivos, Juan Ramón Oreja Rodríguez

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt91j.htm

Website: www.rasch.org/rmt/contents.htm