3PL IRT or Rasch?

When you encounter a complicated data set, do you wonder, ever, whether a 3-parameter model [3PL, 3-PL, three parameter logistic model] would do better than the far simpler Rasch model? Theory sides with Rasch (RMT 6:1 196-200), but does data? Comparison of Rasch results with a more complex and expensive 3PL analysis provides an empirical test of the degree to which 3PL surely must be more informative than Rasch.

See also IRT in the 1990s: which model works best?

The 1992 National Adult Literacy Survey, NALS, rib-spiralled 24,944 adults through a 173 literacy item survey. This produced an 80% empty 173 x 24,944 matrix of dichotomies. ETS reports a 3PL analysis of these data: difficulties and discriminations for the 173 items and "guessing" lower asymptotes for the 13 MCQ items. Each of the 24,944 respondents got 5 "plausible values" randomly selected from each of three posterior ability distributions, reflecting three different types of literacy. The means of each set of 5 are analogous to 3 person measures. Their S.D.s are analogous to S.E.s.

MESA used BIGSTEPS for 90 minutes on a minimal laptop to analyze the same data. This time each respondent got 1 Rasch literacy measure with standard error and fit evaluation. Each item got 1 difficulty calibration with its own standard error and fit evaluation.

When the 3x5=15 3PL "plausible values" (= theta estimates with their error distributions) and 1 Rasch measure are correlated over 24,944 adults, and the (16x15)/2 = 120 raw correlations are disattenuated for measurement error, no correlation is less than .92, and 40 exceed .99! The Rasch measure correlates as highly with the plausible values as they do with each other, even within their homogeneous sets of 5. Principal component analysis of the 16x16 raw correlations finds a 1st factor absorbing 88% of the total variance and a 2nd factor of less than 3%. The Rasch measure is just as good a measure of literacy as any of the plausible values, pointing out that these data only support one literacy measure, not three!

3PL, in notation and practice, is less interested in "incidental" person parameters than in its 3 item parameters. Are there any useful differences between the Rasch and 3PL item results?

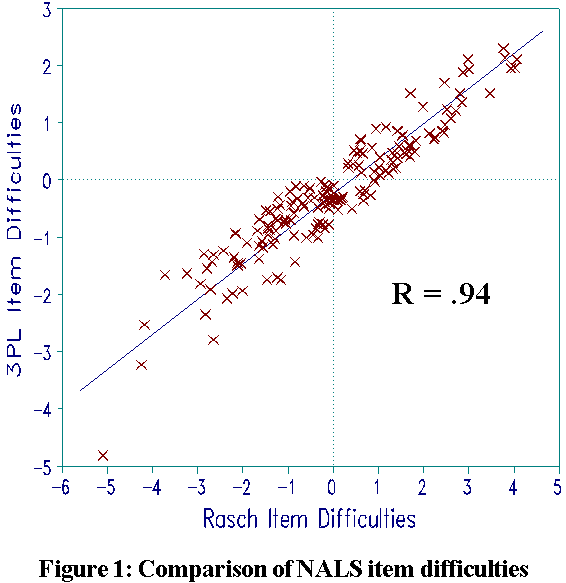
Figure 1 shows that Rasch and 3PL item difficulties correlate .94. Since 3PL difficulties are inevitably perturbed by the attempt to estimate item discriminations from the same data, .94 is a high correlation.

Rasch specifies all items to have the same discrimination. It is this specification which obtains the parameter separation necessary for conjoint additivity, sufficient statistics and the uncrossed ICCs necessary to build a coherent construct definition (RMT 6:1 p. 196-200).

The slopes of empirical ICCs always differ, of course. The inferential question is how to handle these differences? Shall we mistake them for enduring item characteristics to be carried forward in parameter form (as 3PL does)? Or shall we recognize them as local, irreproducible descriptions of how this sample reacted to these items? Conventional raw score item analysis evaluates variation in ICC slope as a sample-dependent point- biserial fit statistic. Rasch analysis takes the same position, but uses the more context-free mean-square-ratio fit statistics.

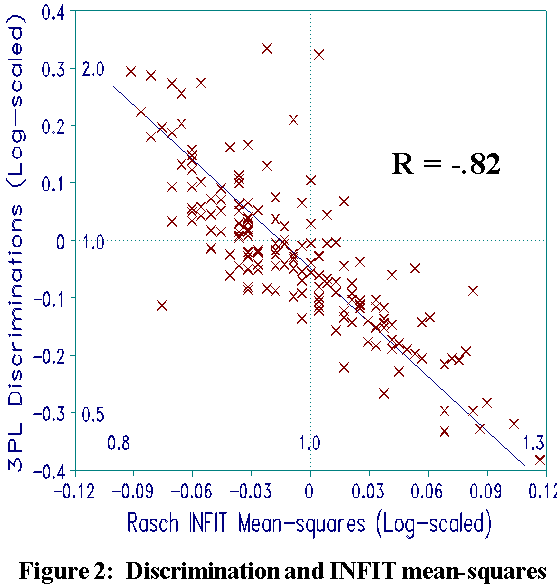
To find the 3PL discriminations in a Rasch analysis one need only examine Rasch item INFIT statistics. Figure 2 shows that 3PL item discrimination (log-scaled) and Rasch item INFIT mean-square (log-scaled) correlate -.82. These two statistics contain the same information:
log_e(3PL discrimination) = -3.3 log_e(INFIT Mnsq)

Nearly all the NALS item INFIT mean-squares are within usual fit criteria (0.8 - 1.2). This means that most of these differences in discrimination can be attributed to random variation, rather than enduring effects. 3PL attempts to use discrimination information as a reproducible characteristic of the item, an inference. Rasch, instead, recognizes its unstable sample dependence as a description of this occasion. Parameterizing discrimination does not clarify item function. Rather, it perpetuates a stochastic, unreplicable aspect of sample behavior.

Sometimes, when Rasch analysis allows credit for lucky guesses, it is accused of bias in favor of low performers. 3PL attempts to counteract item guessability for all respondents, whatever their individual behavior, by introducing a lower asymptote. Lower asymptotes were estimated for the 13 NALS MCQ items. In the Rasch approach, when lucky guessing (unexpected success by low ability respondents) actually does occur, it is detected by item (and person) OUTFIT statistics.

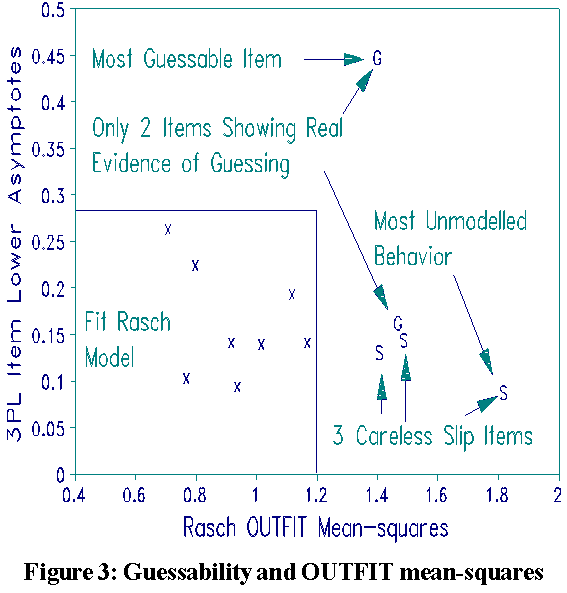
Figure 3 shows that when 3PL lower asymptotes are plotted against Rasch OUTFIT mean-squares almost no guessing occurred in the NALS data. Only 2 of the 13 MCQ items, "G" in Figure 3 (in printed text), show evidence of guessing. In contrast, 3 other MCQ items show evidence of carelessness (unexpected failure by high ability respondents), "S" in Figure 3. The NALS data contain far more unexpected failures than successes. This contraindicates parameterizing lower asymptotes for NALS data.

The bulky and complex NALS data, containing a wide variety of dichotomous item types and administered to a large and diverse sample of respondents, is just the data expected to manifest all the features that would make the superiority of 3PL clear. This parallel NALS analysis shows, however, that 3PL has no benefits over Rasch and some detriments. 3PL ability estimates and item difficulties are statistically equivalent to Rasch measures.

3PL item discrimination provides the same information as the Rasch INFIT statistic, but parameterizing item discrimination complicates estimation. It also inhibits interpretation and use of item difficulties by obscuring the item hierarchy and hence the construct definition.

The lower asymptote is also detrimental. In most cases, there is no lucky guessing, so adding this parameter penalizes all respondents, particularly lower performers who really knew the answer. In the few cases when guessing is actually thought to have occurred, a simple strategy is to remove the easily detectable putative lucky guesses from the data set, treating those few items as not administered to those few people. Then only those who guessed are penalized, and then only by that very small amount by which their lucky guessing boosted their performances.

3PL IRT or Rasch? Wright BD. … Rasch Measurement Transactions, 1995, 9:1 p.408

Rasch Publications
Rasch Measurement Transactions (free, online)	Rasch Measurement research papers (free, online)	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Applying the Rasch Model 3rd. Ed., Bond & Fox	Best Test Design, Wright & Stone
Rating Scale Analysis, Wright & Masters	Introduction to Rasch Measurement, E. Smith & R. Smith	Introduction to Many-Facet Rasch Measurement, Thomas Eckes	Invariant Measurement: Using Rasch Models in the Social, Behavioral, and Health Sciences, George Engelhard, Jr.	Statistical Analyses for Language Testers, Rita Green
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Journal of Applied Measurement	Rasch models for measurement, David Andrich	Constructing Measures, Mark Wilson	Rasch Analysis in the Human Sciences, Boone, Stave, Yale
in Spanish:	Análisis de Rasch para todos, Agustín Tristán		Mediciones, Posicionamientos y Diagnósticos Competitivos, Juan Ramón Oreja Rodríguez

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt91b.htm

Website: www.rasch.org/rmt/contents.htm