PROX for Polytomous Data

PROX for polytomous data. Linacre JM. … 8:4 p.400

The Normal Approximation Estimation Algorithm (PROX) was developed for dichotomous data (Cohen 1979), but can be extended to many-facet polytomous data with missing observations. The expediting specification is that each parameter (e.g., person, item, task, step) is taken to have encountered a symmetrically distributed sample of challenges (e.g., person facing items+tasks+judges). The distributions of challenges faced by the elements may have different means and variances.

Consider the two-facet case of person abilities {B_n} facing item difficulties {D_i} on a rating scale with step calibrations {F_k}, k=0,m. According to Rasch, for each pair of adjacent categories, there is the logistic relationship

Label the logistic function , so that

Count the S_ik persons who respond to item i in category k. Then sum for each item i across all S_ik-1+S_ik persons it encounters, who respond in categories k-1 or k,

Taking the categories in pairs exhausts the data, so accumulate these sums across all odd rating scale steps, k=1,3,..,m,

For convenience, define

When the N_i relevant {B_n-F_k} are symmetrically distributed, summing across them can be approximated by integrating across N_i normal distributions of a random variable {x} with mean µ_i and standard deviation σ_i of the relevant {B_n-F_k}:

where indicates the normal cumulative distribution function.

A convenient equivalence between logistic and normal cumulative distributions (Camilli 1994) is

producing,

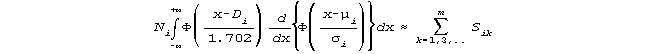
But, in general,

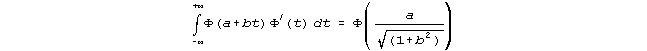
since 1.702² = 2.9,

substituting the logistic for the cumulative normal,

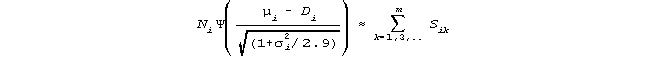
and rearranging, produces an estimation equation for D_i, the logit difficulty of item i,

with standard error

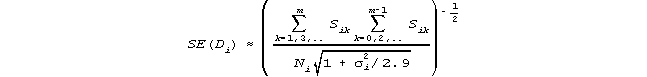
The comparable PROX estimation equation for person n with logit ability, B_n, is

where S_nk is the number of responses in category k by person n, and µ_n and σ_n summarize the distribution of relevant logit difficulties {D_i+F_k} encountered by person n.

A convenient approach is to average the results obtained by considering two sets of even numbers of categories: the upper categories, omitting category 0, with N_iu observations,

and the lower categories, omitting category m, with N_il observations,

so that

with standard error

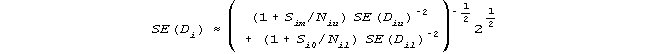
Estimation equations for the step calibrations are

where S_k is the number of responses in category k. µ_k and _k summarize the logit measures {B_n-D_i} for the S_k-i+S_k responses in categories k-1 and k.

If step k is not observed, then F_k=∞, F_k+1=-∞, and F_k+F_k+1 is given by

where k' indicates responses of k-1 or k+1.

These equations can be solved iteratively, with anchoring constraints like D_i0, Fk0, producing estimates for the measures of all elements. For more than two facets, the {µ_i} and {σ_i} summarize the distribution of the combined measures {B_n-..-F_k} of the other facets as encountered by item i, and similarly for the persons, tasks, judges, steps, etc.

John Michael Linacre

Camilli, G. 1994. Origin of the scaling constant d=1.7 in item response theory. Journal of Educational and Behavioral Statistics. 19(3) p.293-5.

Cohen, L. 1979. Approximate expressions for parameter estimates in the Rasch model. British Journal of Mathematical and Statistical Psychology 32(1) 113-120.

PROX for polytomous data. Linacre JM. … Rasch Measurement Transactions, 1995, 8:4 p.400

Rasch-Related Resources: Rasch Measurement YouTube Channel
Rasch Measurement Transactions & Rasch Measurement research papers - free	An Introduction to the Rasch Model with Examples in R (eRm, etc.), Debelak, Strobl, Zeigenfuse	Rasch Measurement Theory Analysis in R, Wind, Hua	Applying the Rasch Model in Social Sciences Using R, Lamprianou	El modelo métrico de Rasch: Fundamentación, implementación e interpretación de la medida en ciencias sociales (Spanish Edition), Manuel González-Montesinos M.
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Rasch Models for Measurement, David Andrich	Constructing Measures, Mark Wilson	Best Test Design - free, Wright & Stone Rating Scale Analysis - free, Wright & Masters
Virtual Standard Setting: Setting Cut Scores, Charalambos Kollias	Diseño de Mejores Pruebas - free, Spanish Best Test Design	A Course in Rasch Measurement Theory, Andrich, Marais	Rasch Models in Health, Christensen, Kreiner, Mesba	Multivariate and Mixture Distribution Rasch Models, von Davier, Carstensen
Rasch Books and Publications: Winsteps and Facets
Applying the Rasch Model (Winsteps, Facets) 4th Ed., Bond, Yan, Heene	Advances in Rasch Analyses in the Human Sciences (Winsteps, Facets) 1st Ed., Boone, Staver	Advances in Applications of Rasch Measurement in Science Education, X. Liu & W. J. Boone	Rasch Analysis in the Human Sciences (Winsteps) Boone, Staver, Yale	Appliquer le modèle de Rasch: Défis et pistes de solution (Winsteps) E. Dionne, S. Béland
Introduction to Many-Facet Rasch Measurement (Facets), Thomas Eckes	Rasch Models for Solving Measurement Problems (Facets), George Engelhard, Jr. & Jue Wang	Statistical Analyses for Language Testers (Facets), Rita Green	Invariant Measurement with Raters and Rating Scales: Rasch Models for Rater-Mediated Assessments (Facets), George Engelhard, Jr. & Stefanie Wind	Aplicação do Modelo de Rasch (Português), de Bond, Trevor G., Fox, Christine M
Exploring Rating Scale Functioning for Survey Research (R, Facets), Stefanie Wind	Rasch Measurement: Applications, Khine	Winsteps Tutorials - free Facets Tutorials - free	Many-Facet Rasch Measurement (Facets) - free, J.M. Linacre	Fairness, Justice and Language Assessment (Winsteps, Facets), McNamara, Knoch, Fan

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt84k.htm

Website: www.rasch.org/rmt/contents.htm