Diagnosing Noisy Anchors

Item bank constructors go to great pains to obtain item calibrations that have exhibited good fit when administered to large, relevant samples of examinees. But what if this isn't possible? What can happen when anchor values are of doubtful quality? We encountered this situation doing "common person" equating. We had a set of persons measured on our standard item bank, who also took a pilot test (of the same construct) that we wanted to equate to the bank. This pilot test had no items in common with our bank. So "common item" equating was out. We tried "common person" equating. A well-known drawback to common person equating is that person abilities are generally less stable than item difficulties. Ability, as it is applied, can change quickly over time! But we tried it anyway. Let's see what happened.

        -2       -1        0        1        2        3
     +---+--------+--------+--------+--------+--------+--+
I    |                      |    1                       |
T   3+                      |                            +
E    |                      |                            |
M    |                      |                            |
     |                     1|   1                        |
    2+----------------------2----------------------------+
I    |                  11  |1                           |
N    |                    11|1                           |
F    |                 1  1 |                            |
I   1+                     1|1          1                +
T    |          1   1    1  21 1  11 1 1                 |
     |                1   1 |     1 22    1 1            |
     |           1      1 221       1    21  1  1        |
S   0+-1--------1----1------|----------1-111------------1+
T    |    111121 21 1  1 1  |1       1                   |
D    |1  111 2     1 1      |    1 1                     |
     |       1 122   11  11 1   2                        |
   -1+      11     11   1  1|1                           +
     |               1    1 |  1                         |
     |                 1 1  | 1                          |
     |                      |                            |
   -2+----------------------|----------------------------+
     |                   1  |                            |
     |                      |                            |
     |                      |                            |
   -3+                     1|                            +
     +---+--------+--------+--------+--------+--------+--+
        -2       -1        0        1        2        3
                       ITEM  MEASURE

Fig. 1. Fit of items to pilot data without anchoring

Figure 1 shows the item fit in the pilot test analyzed in the usual way without anchoring. Fit is distributed in a reasonable way for a test that is targeted on the persons. Perhaps there are 3 or 4 misbehaving items, but not much to worry about. Then we anchored the persons at their bank measures. The fit plot now looks like Figure 2. There is catastrophic misfit! And it is worst for the central items, those most informative about person performance. What has happened?

      -8      -7      -6      -5      -4      -3      -2      -1
     +-+-------+-------+-------+-------+-------+-------+-------+-+
    7+                       2                                   +
I    |                    1  |                                   |
T   6+                      2|1                                  +
E    |                       41                                  |
M   5+                     2 1 111                               +
     |                  11132|  1                                |
    4+                   12111 1 1                               +
I    |                 1 1122|    1  1                           |
N   3+               11 11  1|    11                             +
F    |               211  1  |  1  13  1                         |
I   2+------------21-11------|---1--11-------------------------  +
T    |        1 11131   1    |          11                       |
    1+      1211111  1       |       1 11 31 1                   +
     |    11 1 31 1          |          1 1    1                 |
S   0+--1--------------------|-------------------------1-------  +
T    |                       |                                   |
D  -1+                       |                                   +
     +-+-------+-------+-------+-------+-------+-------+-------+-+
      -8      -7      -6      -5      -4      -3      -2      -1
                          ITEM  MEASURE

                        111324334642
PERSON        42214274491951564826228122 241                11
                    Q    S    M    S    Q

Fig. 2. Person-anchored fit of items to pilot data

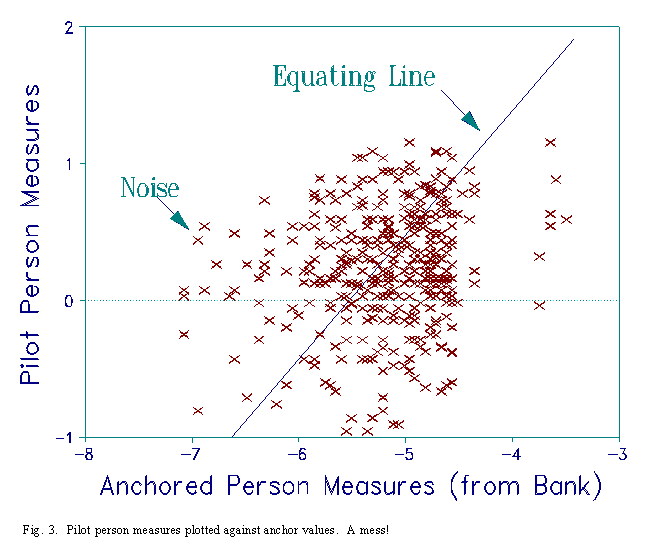
Examination of the two sets of person measures, plotted in Figure 3, reveals all. Their correlation is less than 0.2. Forcing the contradictory anchored person measures on the pilot data has introduced noise into the measurement system. This noise has piled up in the central items, those most sensitive to person disordering, but is less noticeable in the extreme items.

The moral of the story: always choose your anchored elements carefully, particularly if they are persons!

Betty Bergstrom

Diagnosing Noisy Anchors. Bergstrom B. Rasch Measurement Transactions 1994 7:4 p.327

Diagnosing Noisy Anchors. Bergstrom B. … Rasch Measurement Transactions, 1994, 7:4 p.327

Rasch Publications
Rasch Measurement Transactions (free, online)	Rasch Measurement research papers (free, online)	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Applying the Rasch Model 3rd. Ed., Bond & Fox	Best Test Design, Wright & Stone
Rating Scale Analysis, Wright & Masters	Introduction to Rasch Measurement, E. Smith & R. Smith	Introduction to Many-Facet Rasch Measurement, Thomas Eckes	Invariant Measurement: Using Rasch Models in the Social, Behavioral, and Health Sciences, George Engelhard, Jr.	Statistical Analyses for Language Testers, Rita Green
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Journal of Applied Measurement	Rasch models for measurement, David Andrich	Constructing Measures, Mark Wilson	Rasch Analysis in the Human Sciences, Boone, Stave, Yale
in Spanish:	Análisis de Rasch para todos, Agustín Tristán		Mediciones, Posicionamientos y Diagnósticos Competitivos, Juan Ramón Oreja Rodríguez

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt74k.htm

Website: www.rasch.org/rmt/contents.htm