Guessing and Measurement

A frequent worry with multiple-choice questions (MCQ) is the possibility of unearned success by lucky guessing. Studies of guessing behavior report that "the great majority of examinees do not engage in random guessing" and that "difficult items, as might be expected, attract much more guessing than less difficult ones." Consequently, "one can easily hypothesize that when a guesser engages in random guessing, it is only on those items which are too difficult for him" (Waller, 1973). An empirical study confirms this and suggests a simple and convenient solution.

From Johnson O'Connor Research Foundation's bank of 1,294 5-choice MCQ vocabulary items, 17 linked tests of 110 items each were constructed. Each test was administered to 400-600 students. The CAT System Software combined the raw data from these 17 forms into one large data matrix in which responses to items that persons did not encounter were marked as missing. Rasch analysis of this 1,294 item by 7,711 student response matrix produced a measure for each examinee (B) and a calibration for each item (D). The difference between the ability of each examinee and the difficulty of each item encountered (B-D) was calculated for 835,000 valid encounters. [Figure 2 shows their distribution.] Most encounters involved items that were not too hard for examinees (B-D > -1) and so would not provoke random guessing.

Figure 1. Percent-success ogives.

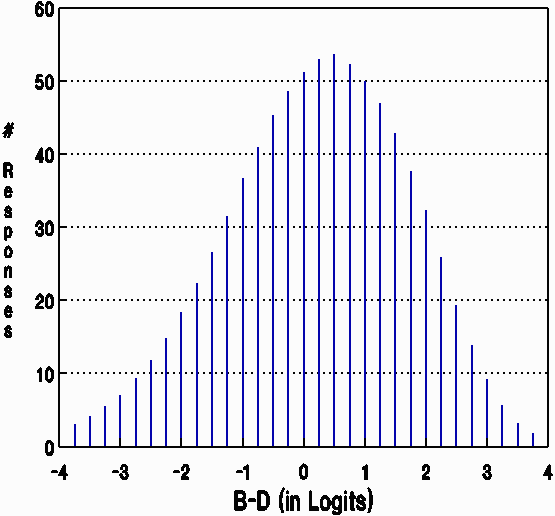Figure 2. Distribution of responses (in thousands).

Nevertheless, some guessing behavior was evident. Figure 1 compares the theoretical and empirical success distributions. The solid ogive is the expected percent success for data fitting the Rasch model. The dotted ogive is the observed success rate for each strata of (B-D). The 15% success rate at the lower asymptote is significantly less than the 20% expected for random guessing on 5-choice MCQ items. Obviously not everyone is guessing.

The effect of guessing on measurement is clear. The bottom left of Figure 1 shows that lucky guesses make some low ability examinees appear more able than they are. Their performance on items too hard for them is better than expected, inflating their measures. This is confirmed in the center of Figure 1 which shows the lucky guessers' observed performance to be worse than expected on items targeted at their inflated abilities. At the top right of Figure 1, observed performance appears better than expected because few low ability guessers (with inflated abilities) encounter items much too easy for them.

The obvious solution to the lucky guessing problem is to remove the provocation to guess. This can be done post-hoc by removing responses to items too hard for an examinee. Figure 1 suggests a useful lower cut- off at -1 logit, i.e., disregard responses when examinees encounter items more than one logit too difficult for them. To safeguard against carelessness provoked by excessively easy items, use an upper cut-off point at +2 logits, i.e., disregard responses when examinees encounter items more than two logits too easy for them. Such cut-offs are easily implemented by the BIGSTEPS/WINSTEPS (CUTLO=, CUTHI=) Rasch analysis computer program.

CUTLO= is equivalent to the procedure outlined in Bruce Choppin. (1983). A two-parameter latent trait model. (CSE Report No. 197). Los Angeles, CA: University of. California, Center for the Study of Evaluation.

Results after eliminating responses outside these cut-points produces the "+" ogive in Figure 1. The "+" ogive includes all observed responses, but its position is based on estimates of B and D from the tailored response set. Since the guessing in the lower tail no longer influences estimation, the "+" ogive is closer to the solid ogive in the center of the range.

After this response tailoring, 110 of the 1,294 items had less than 100 responses or large misfit. These items were dropped, and a new tailored analysis performed. The results are shown by the "." ogive in Figure 1. Now the theoretical and empirical ogives match well enough for all practical purposes in the relevant (-1.25 to +3) region. The removal of measure inflation among low ability performers has also raised the lower asymptote closer to the theoretical guessing level of 20%.

Good item calibration demands that calibrations be based on responses relevant to what the item is intended to measure. Removing responses likely to be contaminated by guessing, carelessness and poor item construction improves the basis for good item calibration. This is particularly relevant when calibrations are used for computer-adaptive testing (CAT), because CAT examinees never experience items much too easy or much too hard. When person measures must be based on entire response strings, a secondary analysis can be performed of all data with item calibrations anchored at their best values.

Gershon R. 1992. The CAT System software program. Chicago: Computer Adaptive Technologies

Waller MI. 1973. Removing the effects of random guessing from latent ability estimates. Ph.D. dissertation. Chicago.

Later note: Andrich et al. (2012) also discover that a lower cut-off near -1 logits is effective in tailoring the data to eliminate the effect of guessing on measurement.
David Andrich, Ida Marais, and Stephen Humphry (2012) Using a Theorem by Andersen and the Dichotomous Rasch Model to Assess the Presence of Random Guessing in Multiple Choice Items Journal of Educational and Behavioral Statistics, 37, 417-442.

Guessing and Measurement, R Gershon … Rasch Measurement Transactions, 1992, 6:2 p. 209-10

Rasch-Related Resources: Rasch Measurement YouTube Channel
Rasch Measurement Transactions & Rasch Measurement research papers - free	An Introduction to the Rasch Model with Examples in R (eRm, etc.), Debelak, Strobl, Zeigenfuse	Rasch Measurement Theory Analysis in R, Wind, Hua	Applying the Rasch Model in Social Sciences Using R, Lamprianou	El modelo métrico de Rasch: Fundamentación, implementación e interpretación de la medida en ciencias sociales (Spanish Edition), Manuel González-Montesinos M.
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Rasch Models for Measurement, David Andrich	Constructing Measures, Mark Wilson	Best Test Design - free, Wright & Stone Rating Scale Analysis - free, Wright & Masters
Virtual Standard Setting: Setting Cut Scores, Charalambos Kollias	Diseño de Mejores Pruebas - free, Spanish Best Test Design	A Course in Rasch Measurement Theory, Andrich, Marais	Rasch Models in Health, Christensen, Kreiner, Mesba	Multivariate and Mixture Distribution Rasch Models, von Davier, Carstensen
Rasch Books and Publications: Winsteps and Facets
Applying the Rasch Model (Winsteps, Facets) 4th Ed., Bond, Yan, Heene	Advances in Rasch Analyses in the Human Sciences (Winsteps, Facets) 1st Ed., Boone, Staver	Advances in Applications of Rasch Measurement in Science Education, X. Liu & W. J. Boone	Rasch Analysis in the Human Sciences (Winsteps) Boone, Staver, Yale	Appliquer le modèle de Rasch: Défis et pistes de solution (Winsteps) E. Dionne, S. Béland
Introduction to Many-Facet Rasch Measurement (Facets), Thomas Eckes	Rasch Models for Solving Measurement Problems (Facets), George Engelhard, Jr. & Jue Wang	Statistical Analyses for Language Testers (Facets), Rita Green	Invariant Measurement with Raters and Rating Scales: Rasch Models for Rater-Mediated Assessments (Facets), George Engelhard, Jr. & Stefanie Wind	Aplicação do Modelo de Rasch (Português), de Bond, Trevor G., Fox, Christine M
Exploring Rating Scale Functioning for Survey Research (R, Facets), Stefanie Wind	Rasch Measurement: Applications, Khine	Winsteps Tutorials - free Facets Tutorials - free	Many-Facet Rasch Measurement (Facets) - free, J.M. Linacre	Fairness, Justice and Language Assessment (Winsteps, Facets), McNamara, Knoch, Fan

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt62a.htm

Website: www.rasch.org/rmt/contents.htm