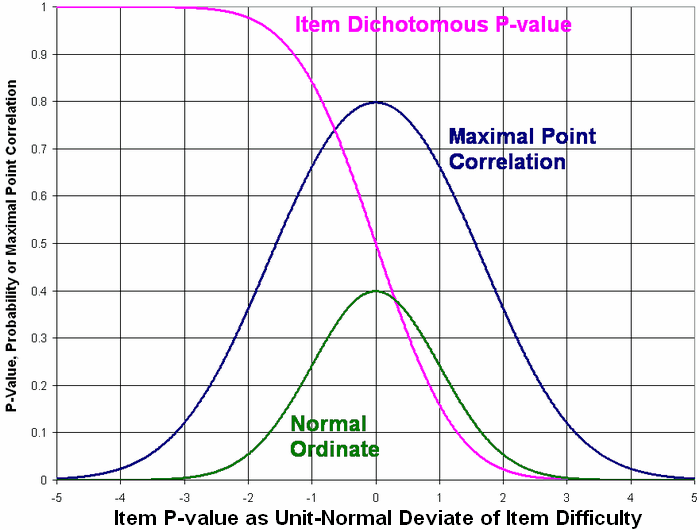
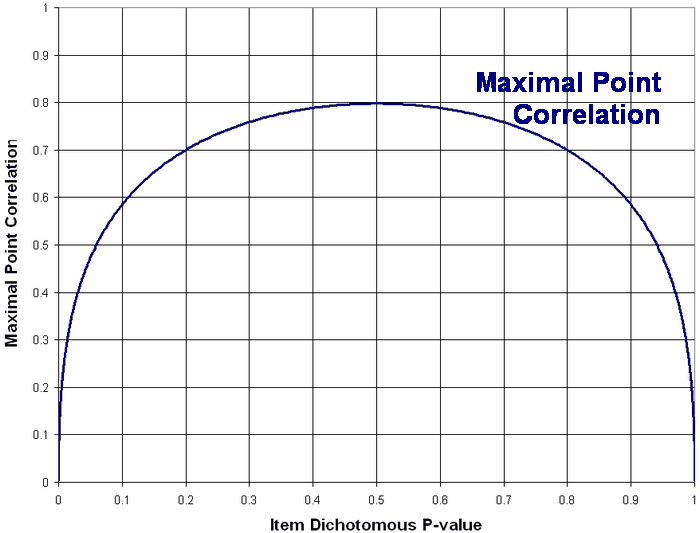
Maximal point-biserial or point-measure correlation is (Normal Ordinate)/square-root(P-Value * (1 - P-Value))
Figure corrected on 7/25/2011
The relation between point-biserial correlation discrimination estimates (rpbis) and Rasch fit statistics (RFS) is nearly monotonic apart from the effect of item-person targeting on point-biserial ceilings.
 Maximal point-biserial or point-measure correlation is (Normal Ordinate)/square-root(P-Value * (1 - P-Value)) Figure corrected on 7/25/2011 |

|
The Figure shows the maximum possible point-biserial correlations with complete dichotomous data for items with different p-values relative to a normally-distributed sample of person abilities.
a. When item response residuals are noisy, disturbed by unexpected variation, they contradict the item's calibration. This makes the item rpbis smaller than typical of these data and the item RFS larger than expected statistically.
b. When item response residuals are muted, subdued by unexpected lack of variation, they indicate a contraction from the modelled level of independence among residuals and hence an underestimation of standard errors of measurement based on this model. This makes the item rpbis larger than typical of these data and the item RFS smaller than expected statistically.
There is an important difference in the utility of these alternative fit statistics. For the rpbis based on raw scores, the most we can say is "smaller (or larger) than we are used to". We don't know where the value we are observing is placed in the possible range. We don't know whether that value is acceptable, undesirably large or undesirably small. The rpbis is a misfit statistic but of unknown size and significance. All we know for certain, (and this is useful in detecting miscoded data), is that negative rpbis means that the observed responses to that item contradict the general meaning of the test.
For RFS based on a measurement system, we can say - "larger (or smaller) than expected statistically". The basis for expectation is a statistical model for a standard distribution of residuals. RFS give a size and a significance to misfit. The size enables us to identify misfit big enough to disturb measurement. The significance indicates what proportion of all possible misfit statistics would be better fitting than this one.
One author writes: "Ideally, it is recommended that items have point-biserials ranging from 0.30 to 0.70
(Allen, M. J. and Yen, W. M. (1979). Introduction to Measurement Theory. Waveland Press, Inc. Prospect Heights Il)".
A rule such as this cuts off the very easy and very hard items, and may even eliminate good-fitting on-target items.
Point-biserials and item fits. Wright BD. … Rasch Measurement Transactions, 1992, 5:4 p.174
| Forum | Rasch Measurement Forum to discuss any Rasch-related topic |
Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement
Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.
| Coming Rasch-related Events | |
|---|---|
| Jan. 16 - Feb. 13, 2025, Fri.-Fri. | On-line workshop: Rasch Measurement - Core Topics (E. Smith, Winsteps), www.statistics.com |
| Apr. 8 - Apr. 11, 2026, Wed.-Sat. | National Council for Measurement in Education - Los Angeles, CA, ncme.org/events/2026-annual-meeting |
| Apr. 8 - Apr. 12, 2026, Wed.-Sun. | American Educational Research Association - Los Angeles, CA, www.aera.net/AERA2026 |
| May. 15 - June 12, 2026, Fri.-Fri. | On-line workshop: Rasch Measurement - Core Topics (E. Smith, Winsteps), www.statistics.com |
| June 19 - July 25, 2026, Fri.-Sat. | On-line workshop: Rasch Measurement - Further Topics (E. Smith, Winsteps), www.statistics.com |
The URL of this page is www.rasch.org/rmt/rmt54a.htm
Website: www.rasch.org/rmt/contents.htm