CAT with a Poorly Calibrated Item Bank

A dogma of CAT is that "good estimates of the item parameters are required" (Vale & Giaculla 1988). But how good? The practical answer, namely, that an educated guess is good enough (Wright & Panchapakesan, 1969; Wright & Douglas, 1976), has been confirmed again.

The U.S. Department of Education is supporting the development of a Mac-based CAT program for literacy in Chinese. The graphics of the Mac make displaying Chinese characters easy. Hypercard software is ideal for administering multiple-choice items. All that is needed is a Hypercard algorithm for item administration and person measurement.

Before data were collected, Chinese language experts categorized 69 newly-written test items according to 9 levels of GSA language proficiency. These conceptual levels served as the assigned item difficulty calibrations.

A simple two-stage CAT "Step Ladder" algorithm was used (Henning 1987 p.138). First, an easy, medium and hard item were administered to determine which of the 9 levels was the best starting level for the second phase. Then item administration began at the indicated starting level. Success raised the level of administration, failure lowered it. The test stopped when the examinee achieved over 50% success (including at least four correct responses) at one level, but less than 50% success (including at least four incorrect responses) at the level above. The examinee's GSA rating was this "success" level.

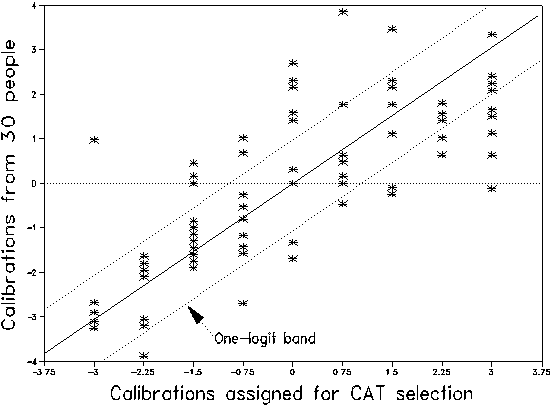
The psychometric question is how much does this non-empirical assigned calibration of the items distort the person measures? Two Rasch analyses were performed. The first produced measures for the 30 examinees based on the assigned calibrations with levels placed an arbitrary 0.75 logits apart. The second produced person measures and empirical item calibrations based solely on the responses. Figure 1 plots the alternative item calibrations against one another. The assigned mis-calibration of certain items is clear. The average absolute item calibration difference is 1.0 logits, showing that the assigned calibration was a poor predictor of empirical calibration. Figure 2 plots the alternative sets of person measures against one another. None of these points lie outside 95% confidence bands. Note that none are significantly different. The slight non-linearity of the measures is caused by the arbitrary 0.75 logit spacing of the assigned levels. Conclusion: precise item calibration is not required for usefully accurate CAT person measurement!

Henning G 1987. A guide to language testing. Cambridge, Mass.: Newbury House

Vale CD & Giaculla KA 1988. Evaluation of the efficiency of item calibration. Applied Psychological Measurement 12 53-67.

Wright B & Panchapakesan N 1969. A procedure for sample-free item analysis. Educational & Psychological Measurement 29 1 23-48

Wright B & Douglas G 1975. Best test design and self-tailored testing. MESA Memorandum No. 19. Department of Education, Univ. of Chicago

Wright, B. D. & Douglas, G. A. Rasch item analysis by hand. Research Memorandum No. 21, Statistical Laboratory, Department of Education, University of Chicago, 1976

Wright & Douglas(1976) "Rasch Item Analysis by Hand": "In other work we have found that when [test length] is greater than 20, random values of [item calibration] as high as 0.50 have negligible effects on measurement."

Wright & Douglas (1975) "Best Test Design and Self-Tailored Testing": "They allow the test designer to incur item discrepancies, that is item calibration errors, as large as 1.0. This may appear unnecessarily generous, since it permits use of an item of difficulty 2.0, say, when the design calls for 1.0, but it is offered as an upper limit because we found a large area of the test design domain to be exceptionally robust with respect to independent item discrepancies."

Wright & Stone (1979) "Best Test Design" p.98 - "random uncertainty of less than .3 logits," referencing MESA Memo 19: Best Test and Self-Tailored Testing. Benjamin D. Wright & Graham A. Douglas, 1975 . Also .3 logits in Solving Measurement Problems with the Rasch Model. Journal of Educational Measurement 14 (2) pp. 97-116, Summer 1977 (and MESA Memo 42)

Figure 1. Plot of item calibrations.

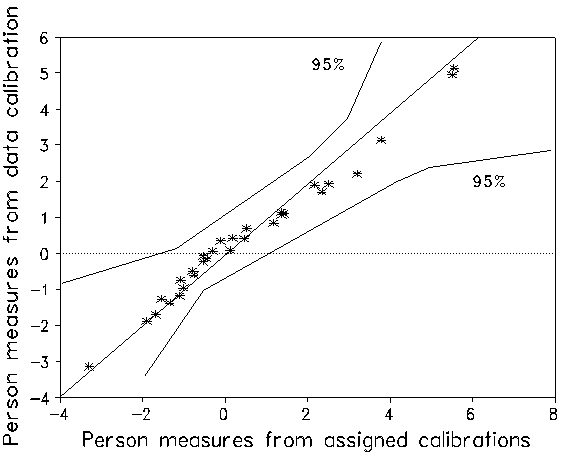Figure 2. Plot of person measures

CAT with a Poorly Calibrated Item Bank, T Yao & J.M. Linacre … Rasch Measurement Transactions, 1991, 5:2 p. 141

Rasch Publications
Rasch Measurement Transactions (free, online)	Rasch Measurement research papers (free, online)	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Applying the Rasch Model 3rd. Ed., Bond & Fox	Best Test Design, Wright & Stone
Rating Scale Analysis, Wright & Masters	Introduction to Rasch Measurement, E. Smith & R. Smith	Introduction to Many-Facet Rasch Measurement, Thomas Eckes	Invariant Measurement: Using Rasch Models in the Social, Behavioral, and Health Sciences, George Engelhard, Jr.	Statistical Analyses for Language Testers, Rita Green
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Journal of Applied Measurement	Rasch models for measurement, David Andrich	Constructing Measures, Mark Wilson	Rasch Analysis in the Human Sciences, Boone, Stave, Yale
in Spanish:	Análisis de Rasch para todos, Agustín Tristán		Mediciones, Posicionamientos y Diagnósticos Competitivos, Juan Ramón Oreja Rodríguez

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt52b.htm

Website: www.rasch.org/rmt/contents.htm