Investigating Guessing Strategies and Their Success Rates on Items of Varying Difficulty Levels

Psychometricians have long known that guessing is a major threat to the validity of a test score and can be a source for construct irrelevant variance. Guessing behaviors typically are investigated in a number of ways, but almost all involve administering an exam to an appropriate sample and investigating the scores and response patterns for clues that guessing might have occurred. At the University of North Carolina at Chapel Hill, we wanted to evaluate the psychometric integrity of our medical school exam items. In doing so, we opted to construct an exam consisting of actual medical school items and administer them to university staff in the Office of Medical Education. It was theorized that the sample would need to rely almost entirely on guessing strategies as none of the participants had any formal educational or experiential training in medicine or the health sciences. By intentionally offering an exam to an inappropriate sample we were able to more deliberately investigate guessing, identify which exam items were vulnerable to testwiseness, and better discern how guessing might impact the quality of our medical students' test scores.

Study Design

As part of our experiment, a purposeful mix of easy, moderate, and difficult items were randomly pulled from each of the courses that comprise the first two years (pre- clinical) of the medical school curriculum. Criteria for determining easy, moderate, and difficult items were arbitrarily categorized by the following schema. Easy items were those that were answered correctly by 76% or more of medical students; moderately difficult items were those that were answered correctly by 51%-75% of medical students; and difficult items were those that were answered correctly by less than 50% of medical students. The exam consisted of a total of 63 items and was administered to 14 professional staff personnel in the Office of Medical Education. A requirement for participation in the study was that all staff must hold at least a bachelor's degree and have no formal educational or experiential training in the physical, life, or health sciences that might unduly offer an advantage on the exam. These criteria for inclusion were necessary so as to assess primarily guessing behaviors with minimal influence of content knowledge.

Accompanying each item was a follow-up question that asked test-takers to rate the extent to which they relied on guessing strategies to answer the previous question. Using Rogers (1999) framework for guessing, we asked test- takers to indicate whether they relied on random, cued, or informed guessing, or no guessing at all. Specifically, we provided the following item:

Please identify the strategy you used to answer the previous question from the options below:

1. I did not guess.
2. Informed guessing: I selected a particular answer based upon previous partial knowledge of the subject, or I was able to eliminate particular answer options based upon previous partial knowledge of the subject.
3. Cued guessing: I selected an answer based upon some sort of stimulus within the test such as wording cues, cues associated with item stems, choices among answer options, testwiseness, etc.
4. Random guessing: I selected a particular answer by blindly choosing an answer.

Results

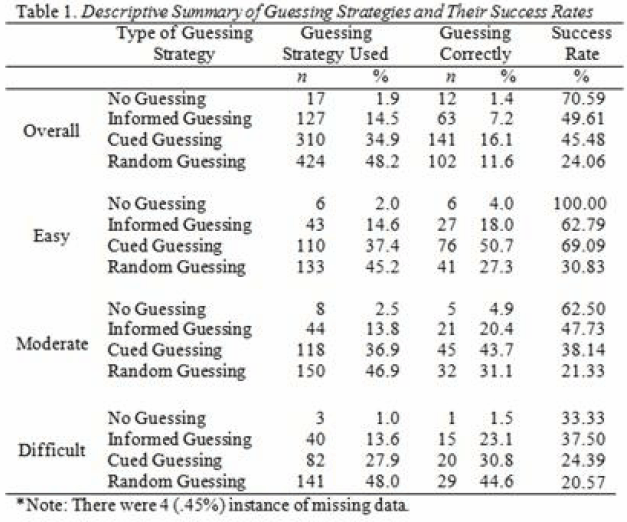
Overall, results reveal a mix of guessing strategies were used. Table 1 presents information regarding the use and success of each guessing strategy. Participants reported they did not guess on 17 items, but the success rate for this strategy indicates they were correct only 70% of the time. Random guessing was used most frequently (nearly half the time), but resulted in the lowest success rate (around 24%). Cued and informed guessing resulted in nearly equal success rates (45-49%).

To take the analysis a step farther, we investigated guessers' performance based on item difficulty. Using the aforementioned criteria for easy, moderate, and difficult items, guessing strategies were investigated to determine which type of guessing resulted in the best success rate relative to item difficulty. Results indicate the easy items are highly vulnerable to guessing. Such high levels of contamination certainly threaten the validity of the information obtained from these items. Interestingly, cued guessing strategies resulted in a slightly higher success rate on easy items than having informed knowledge. However, as the difficulty of the items increased, success rates between cued and informed guessing strategies tended to shift towards informed guessing providing the greater probability of success. The gap between the success rates of informed guessing over cued guessing also widened when the items became more difficult.

According to Rasch measurement theory, a more knowledgeable person should always have a greater probability of success on any item than someone that is less knowledgeable. Because cued guessing (less knowledge) can result in a greater probability of success on easier items than informed guessing (some partial knowledge), this violates Rasch theory. Results presented here illustrate the necessity for good, sound items that are not susceptible to testwiseness strategies.

Additional Considerations and Recommendations

Guessing can impact virtually any test score. Even the best psychometrically functioning exams result in test- takers having a minimum of 20-25% chance of getting any given item correct when presented with four to five response options. Despite the ever-present threat to validity, it remains unclear to what extent guessing threatens the validity of test scores for persons/organizations that do not have a great deal of psychometric expertise and/or editorial resources. Professional testing organizations go to great pains to produce items that are as "bulletproof" as possible, but for others offering moderate to high-stakes exams, this is not always feasible. It is likely the threat to exam score validity is even greater in such situations.

Organizations without sophisticated psychometric expertise would be wise to securely administer their exams to a sample of savvy test-takers in an effort to determine the extent to which the exam items are susceptible to guessing strategies. By asking examinees to provide the type of guessing strategy they used to respond to each item one can get a reasonable estimate of how much guessing is a threat to one's exam. Items deemed particularly problematic, or contaminated, could then be revised and administered on future exams. With proper equating, one could evaluate the effectiveness of the attempt to remove guessing contamination by Rasch analyzing the data and comparing the probability of success on the revised item relative to the item in its initial form. If the item's difficulty estimate increases after the revision, it is likely the revision was successful in removing much of the guessing contamination.

References

Rogers, H. J. (1999). Guessing in multiple-choice tests. In G. N. Masters and J. P. Keeves (Eds.). Advances in measurement in educational research and assessment. (pp. 23-42) Oxford, UK: Pergamon.

Kenneth D. Royal and Mari-Wells Hedgpeth
University of North Carolina at Chapel Hill

Suggestions for Improving AERA's Peer Review Process and Quality of Symposia. William P. Fisher, Jr. … Rasch Measurement Transactions, 2013, 27:1 p. 1408-9

Rasch Books and Publications
Invariant Measurement: Using Rasch Models in the Social, Behavioral, and Health Sciences, 2nd Edn. George Engelhard, Jr. & Jue Wang	Applying the Rasch Model (Winsteps, Facets) 4th Ed., Bond, Yan, Heene	Advances in Rasch Analyses in the Human Sciences (Winsteps, Facets) 1st Ed., Boone, Staver	Advances in Applications of Rasch Measurement in Science Education, X. Liu & W. J. Boone	Rasch Analysis in the Human Sciences (Winsteps) Boone, Staver, Yale
Introduction to Many-Facet Rasch Measurement (Facets), Thomas Eckes	Statistical Analyses for Language Testers (Facets), Rita Green	Invariant Measurement with Raters and Rating Scales: Rasch Models for Rater-Mediated Assessments (Facets), George Engelhard, Jr. & Stefanie Wind	Aplicação do Modelo de Rasch (Português), de Bond, Trevor G., Fox, Christine M	Appliquer le modèle de Rasch: Défis et pistes de solution (Winsteps) E. Dionne, S. Béland
Exploring Rating Scale Functioning for Survey Research (R, Facets), Stefanie Wind	Rasch Measurement: Applications, Khine	Winsteps Tutorials - free Facets Tutorials - free	Many-Facet Rasch Measurement (Facets) - free, J.M. Linacre	Fairness, Justice and Language Assessment (Winsteps, Facets), McNamara, Knoch, Fan
Other Rasch-Related Resources: Rasch Measurement YouTube Channel
Rasch Measurement Transactions & Rasch Measurement research papers - free	An Introduction to the Rasch Model with Examples in R (eRm, etc.), Debelak, Strobl, Zeigenfuse	Rasch Measurement Theory Analysis in R, Wind, Hua	Applying the Rasch Model in Social Sciences Using R, Lamprianou	El modelo métrico de Rasch: Fundamentación, implementación e interpretación de la medida en ciencias sociales (Spanish Edition), Manuel González-Montesinos M.
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Rasch Models for Measurement, David Andrich	Constructing Measures, Mark Wilson	Best Test Design - free, Wright & Stone Rating Scale Analysis - free, Wright & Masters
Virtual Standard Setting: Setting Cut Scores, Charalambos Kollias	Diseño de Mejores Pruebas - free, Spanish Best Test Design	A Course in Rasch Measurement Theory, Andrich, Marais	Rasch Models in Health, Christensen, Kreiner, Mesba	Multivariate and Mixture Distribution Rasch Models, von Davier, Carstensen

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt271d.htm

Website: www.rasch.org/rmt/contents.htm