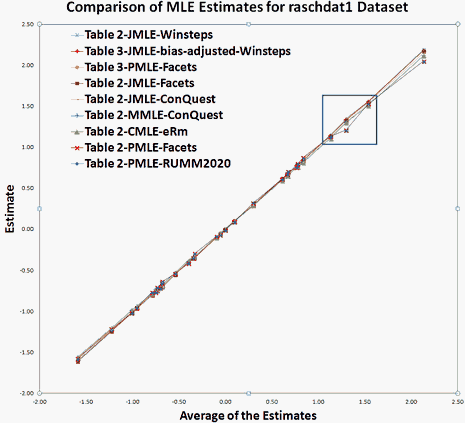
Figure 1. MLE estimates for raschdat1
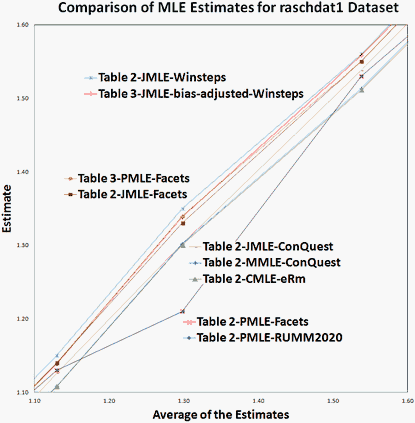
Figure 2. MLE estimates for raschdat1 (Excerpt).
Three riverboat gamblers, Bruce, George and Ben, are discussing tomorrow's sharpshooting contest between Annie Oakley and Lillian Smith. Today's Deadwood Pioneer newspaper contains reports of their previous contests in Table 1 and of their contests with Frank Butler in Table 2.
| Table 1. Previous Contests between Annie and Lillian. (1 = Winner) | Table 2. Previous Contests between Annie or Lillian and Frank. (1 = Winner) | |||||
|---|---|---|---|---|---|---|
| Year | Annie | Lillian | Year | Annie | Lillian | |
| 1888 | 1 | 0 | 1888 | 1 | 0 | |
| 1887 | 0 | 1 | 1887 | 0 | 1 | |
| 1886 | 1 | 0 | 1886 | 1 | 0 | |
| Shooter's Score | 2 | 1 | Shooter's Score | 2 | 1 | |
"Tomorrow it's Annie against Lillian. Here's how to get the odds correct." says Bruce. "Let's use PMLE1. In each Table, Annie and Lillian were in the same situation three times, once for each row. Annie won twice. Lillian won once. The odds in both Tables are 2/1. Annie and Lillian are ln(2/1) = 0.69 logits apart."
"We get those same odds of 2/1 from both Tables using CMLE2,3." agrees George.
"JMLE4 and MMLE5 estimate that the odds for both Tables are 4/1" says Ben. "To produce the correct odds of 2/1 for the direct pairwise comparison of Annie and Lillian in Table 1, we must adjust for JMLE estimation bias6. However, the odds for the indirect pairwise comparison of Annie and Lillian in Table 2 are 4/1. JMLE/MMLE are correct. There is no JMLE estimation bias for Table 2."
"No! No!" objects George. "JMLE estimates are always biased7, even though the bias reduces quickly for larger datasets8. Ben, you are way off target!"
| Table 3. Previous Contests between Annie or Lillian and Frank (redrawn). (1 = Winner) | |||
|---|---|---|---|
| Year | Annie | Frank | Lillian |
| 1888 | 1 | 0 | |
| 1887 | 0 | 1 | |
| 1886 | 1 | 0 | |
| 1888 | 1 | 0 | |
| 1887 | 0 | 1 | |
| 1886 | 1 | 0 | |
| Shooter's Score | 2 of 3 | 3 of 6 | 1 of 3 |
"It's you guys who can't shoot straight" says Ben. "Let's redraw Table 2 so that each row is a separate contest of sharpshooters. Here it is in Table 3 where all the participants are columns and there is one row for each pairwise contest, exactly like Table 1. Let's take Bruce's PMLE logic for Table 1 and apply it to Table 3. All the row scores are 1. In the upper three contests, Annie scores 2 and Frank scores 1. The odds are 2/1 for Annie against Frank. In the lower three contests, Frank scores 2 and Lillian scores 1. The odds are 2/1 for Frank against Lillian. Combining these, the odds for Annie against Lillian are (2/1) * (2/1) = 4/1. They are ln(4/1) = 1.39 logits apart, exactly as JMLE tell us!"
"That is exciting!" exclaims Bruce. "We can extend Table 3 to much larger competitive situations such as Basketball9 and Tennis using PMLE or bias-adjusted JMLE10."
"Ben, why didn't you explain this to me years ago?" says George. "In Tables 1 and 3, the paired comparisons are direct. In Table 2 the comparisons are indirect. Table 2 is an abbreviated version of Table 3. When we treat the comparisons in Table 2 as direct, we distort the meaning of the data, resulting in biased estimates."
"Exactly!" says Ben, "When a dataset is directly pairwise, as in Tables 1 and 3, CMLE/PMLE estimates are accurate and unbiased. We must bias-adjust JMLE estimates. For a dataset of indirect comparisons like Table 2, JMLE estimates are unbiased. CMLE/PMLE estimates for any dataset are biased if reformatting that dataset to be directly pairwise produces different CMLE/PMLE estimates."
Dear Reader: Would you like more evidence? raschdat1.rda is a dichotomous dataset of 30 items and 100 persons distributed in the eRm package. In www.rasch.org/rmt/a/shootout.zip, there are conventional Table 2 (30x100) versions of raschdat1 for CMLE, JMLE, MMLE, and PMLE, also Table 3 pairwise (130x3000) versions for JMLE and PMLE, together with their estimates (see Figure 1) and the Excel worksheet of the Figures. In Figure 2, Table 3 curves track with Table 2 JMLE curves, confirming Ben's claim that JMLE is unbiased for conventional datasets.
 Figure 1. MLE estimates for raschdat1 |
 Figure 2. MLE estimates for raschdat1 (Excerpt). |
John Michael Linacre
Gregory Chan (RUMM2020 Analyses)
Raymond J. Adams (ConQuest analyses)
Endnotes:
1. PMLE, Pairwise Maximum Likelihood Estimation, in RUMM2030 and Facets.
2. CMLE, Conditional Maximum Likelihood Estimation, in eRm.
3. CMLE for Tables 1 and 2: All the rows are scored 1 on the 2 items, so we only need the probabilities for a row score of 1. Let's call P(10) the probability that Annie wins and Lillian loses, then P(01) is the opposite. For each row the total probability for a score of 1 is P(10) + P(01). In each Table, Annie scored 2 in 3 attempts, so 2 = 3 * P(10) / (P(10) + P(01)). Lillian scored 1 in 3 attempts, so 1 = 3 * P(01) / (P(10) + P(01)). Now, divide those two equations, then the odds are P(10)/P(01) = 2/1. ln(2/1) = 0.69 logits.
4. JMLE, Joint Maximum Likelihood Estimation, in ConQuest, Facets and Winsteps. The JMLE estimates are the ones for which the observed marginal score equals the expected marginal score for each row and column.
5. MMLE, Marginal Maximum Likelihood Estimation, in ConQuest. MMLE estimates are the ones for which the observed marginal score for each column equals the expected marginal score, and the row parameters are modeled to have a normal distribution.
6. Using Winsteps, JMLE pairwise estimation bias is adjusted by Paired=Yes
7. Andersen E.B. (1970) Asymptotic properties of conditional maximum likelihood estimators. Journal of the Royal Statistical Society B 32, 283-301
8. Wright, B.D. (1988) The efficacy of unconditional maximum likelihood bias correction: Comment on Jansen, Van den Wollenberg, and Wierda. Applied Psychological Measurement, 12, 315-318. www.rasch.org/memo45.htm
9. Linacre J.M. (2001) Paired comparisons for measuring team performance. RMT, 15:1, 812. www.rasch.org/rmt/rmt151w.htm
10. Linacre J.M. (1997) Paired comparisons with standard Rasch software. RMT, 11:3, 584-5. www.rasch.org/rmt/rmt113o.htm
Available Rasch software is listed at www.rasch.org/software.htm.
Linacre J.M., Chan G., Adams R.J. (2013) An "Estimation Bias" Shootout in the Wild West: CMLE, JMLE, MMLE, PMLE. Rasch Measurement Transactions, 27:1 p.1403-5
| Forum | Rasch Measurement Forum to discuss any Rasch-related topic |
Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement
Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.
| Coming Rasch-related Events | |
|---|---|
| Jan. 16 - Feb. 13, 2025, Fri.-Fri. | On-line workshop: Rasch Measurement - Core Topics (E. Smith, Winsteps), www.statistics.com |
| Apr. 8 - Apr. 11, 2026, Wed.-Sat. | National Council for Measurement in Education - Los Angeles, CA, ncme.org/events/2026-annual-meeting |
| Apr. 8 - Apr. 12, 2026, Wed.-Sun. | American Educational Research Association - Los Angeles, CA, www.aera.net/AERA2026 |
| May. 15 - June 12, 2026, Fri.-Fri. | On-line workshop: Rasch Measurement - Core Topics (E. Smith, Winsteps), www.statistics.com |
| June 19 - July 25, 2026, Fri.-Sat. | On-line workshop: Rasch Measurement - Further Topics (E. Smith, Winsteps), www.statistics.com |
The URL of this page is www.rasch.org/rmt/rmt271a.htm
Website: www.rasch.org/rmt/contents.htm