Should Woodcock's Test Design Nomograph be Adjusted and Applied to Polytomous Tests?

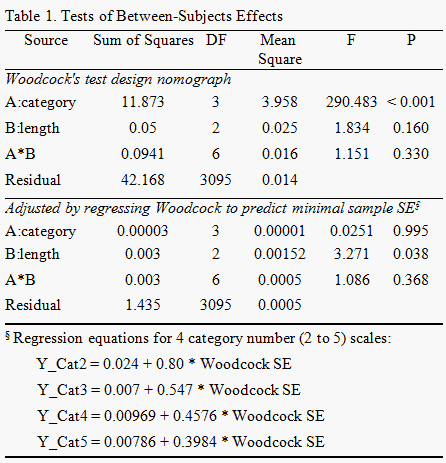
Woodcock's test design nomograph helps construct dichotomous tests (Woodcock, 1992). The computation of Woodcock's nomograph was reported by Pedler (1993) and helped us predict an estimated person logit standard error at a test's center based on item length, and logit range of a uniform test. This prompted us to use a simulation to examine whether Woodcock's expected SE values could be exactly applied to not only dichotomous tests, but also polytomous tests.

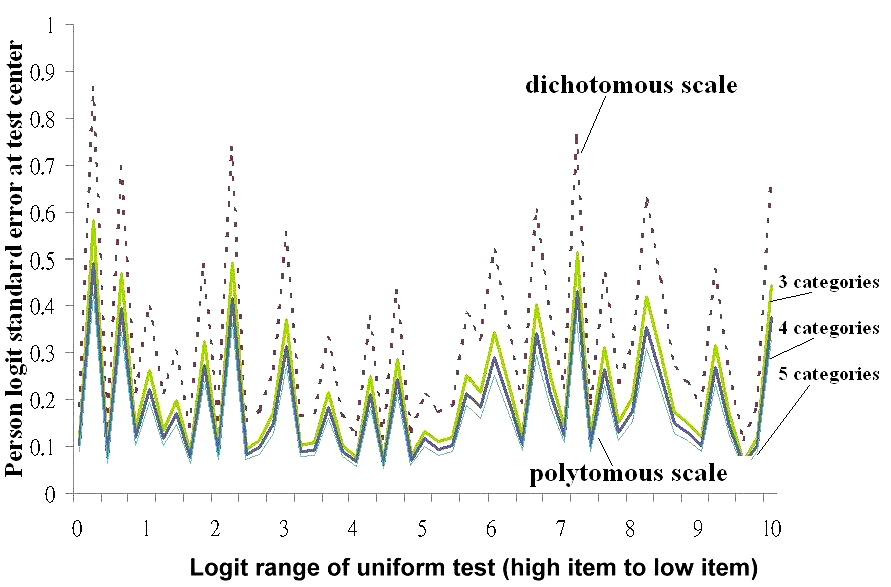
We found Woodcock's test design nomograph cannot be directly applied to both dichotomous and polytomous tests (p < 0.001) (see Table 1). Instead, the adjusted formula (regressing Woodcock SE value to predict Rasch minimal sample logit SE) can be feasibly and optimally useful while using item length with different types of category numbers and the logit ranges to predict a person logit SE at a test's center. Dichotomous scales are statistically significantly different from the polytomous with regards to the expected SEs. In contrast, there are no statistically significant difference between polytomous scales (Figure 1).

A polytomous item of m ordered categories contains m-1 dichotomous category boundaries (Linacre, 2000). A test of k items contains C_k - k dichotomous items. The number of active categories in the known test is shown as below:

Figure 1. Comparison of Woodcock's test for SE by category number of a scale

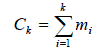
Tsair-Wei Chien, Chi Mei Medical Center, Taiwan
Jianfang Zou, Academy of Medical Science, Shandong, China

References

Woodcock, R. W. (1992). Woodcock test construction nomograph. Rasch Measurement Transactions, 6(3), 243-244. Available at: www.rasch.org/rmt/rmt63p.htm

Pedler, P. (1993). Computerizing Woodcock's test construction nomograph. Rasch Measurement Transactions, 6(4), 255. Available at: www.rasch.org/rmt/rmt64f.htm

Linacre, J.M. (2000). Predicting reliabilities and separations of different length tests. Rasch Measurement Transactions, 14(3), 767. Available at: www.rasch.org/rmt/rmt143j.htm

Should Woodcock's Test Design Nomograph be Adjusted and Applied to Polytomous Tests? Tsair-Wei Chien & Jianfang Zou … Rasch Measurement Transactions, 2013, 26:4 p. 1394-5

Rasch-Related Resources: Rasch Measurement YouTube Channel
Rasch Measurement Transactions & Rasch Measurement research papers - free	An Introduction to the Rasch Model with Examples in R (eRm, etc.), Debelak, Strobl, Zeigenfuse	Rasch Measurement Theory Analysis in R, Wind, Hua	Applying the Rasch Model in Social Sciences Using R, Lamprianou	El modelo métrico de Rasch: Fundamentación, implementación e interpretación de la medida en ciencias sociales (Spanish Edition), Manuel González-Montesinos M.
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Rasch Models for Measurement, David Andrich	Constructing Measures, Mark Wilson	Best Test Design - free, Wright & Stone Rating Scale Analysis - free, Wright & Masters
Virtual Standard Setting: Setting Cut Scores, Charalambos Kollias	Diseño de Mejores Pruebas - free, Spanish Best Test Design	A Course in Rasch Measurement Theory, Andrich, Marais	Rasch Models in Health, Christensen, Kreiner, Mesba	Multivariate and Mixture Distribution Rasch Models, von Davier, Carstensen
Rasch Books and Publications: Winsteps and Facets
Applying the Rasch Model (Winsteps, Facets) 4th Ed., Bond, Yan, Heene	Advances in Rasch Analyses in the Human Sciences (Winsteps, Facets) 1st Ed., Boone, Staver	Advances in Applications of Rasch Measurement in Science Education, X. Liu & W. J. Boone	Rasch Analysis in the Human Sciences (Winsteps) Boone, Staver, Yale	Appliquer le modèle de Rasch: Défis et pistes de solution (Winsteps) E. Dionne, S. Béland
Introduction to Many-Facet Rasch Measurement (Facets), Thomas Eckes	Rasch Models for Solving Measurement Problems (Facets), George Engelhard, Jr. & Jue Wang	Statistical Analyses for Language Testers (Facets), Rita Green	Invariant Measurement with Raters and Rating Scales: Rasch Models for Rater-Mediated Assessments (Facets), George Engelhard, Jr. & Stefanie Wind	Aplicação do Modelo de Rasch (Português), de Bond, Trevor G., Fox, Christine M
Exploring Rating Scale Functioning for Survey Research (R, Facets), Stefanie Wind	Rasch Measurement: Applications, Khine	Winsteps Tutorials - free Facets Tutorials - free	Many-Facet Rasch Measurement (Facets) - free, J.M. Linacre	Fairness, Justice and Language Assessment (Winsteps, Facets), McNamara, Knoch, Fan

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt264d.htm

Website: www.rasch.org/rmt/contents.htm