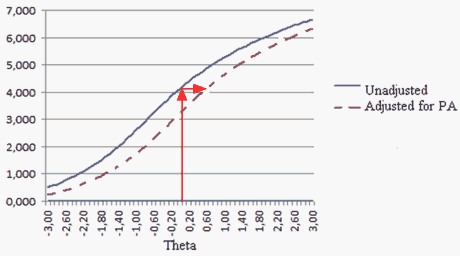
Figure 1. Test Characteristic Curves for both analyses
Do situational factors during measurement change measurement estimates (item difficulties, person abilities, standard errors, etc.)? Our research shows that item difficulties are different when one accounts for individual differences in positive affectivity during test administration. We calibrated the items of a Spelling Instrument ignoring, and then including, the influence of positive affectivity. A two-level Hierarchical Generalized Linear Model (HGLM) was used:
Level-1 (Bernoulli) Rasch model for a test of i = 1,k dichotomous items:
log ( pij / (1-pij) ) = β0j + β1jX1j + ... + βijXij + ... + β(k-1)jX(k-1)j
where pij is the probability that person j will answer item i correctly. β0j is person ability relative to item k and is the intercept of the model. β1j is the easiness of the item 1 (relative to item k) for person j and the coefficient of dummy variable X1. For pij, all the dummy variables are 0, except for Xij = 1 which flags that this equation models a response to item i.
Level-2 model expressing person and item estimates:
β0j = γ00 + u0j
β1j = γ10; ... ; βij = γi0; ... ; β(k-1)j = γ(k-1)0
γ00 is the mean of the person ability distribution relative to item k. u0j is the value of the random ability effect specific to person j. {u0j} are modeled to be normally distributed, N(0,t), across the person sample. The item easinesses, {γi0} are modeled to be invariant across the sample. When this two-level model is applied to the response by person j to item i, the probability of a correct response becomes:
log ( pij / (1-pij) ) = γ00 + γi0 + u0j
In the analysis of our 7-item test of spelling ability, k = 7.
In a second "adjusted" analysis, the Level-2 model was modified by adding the term γ01*PositiveAffectj to β0j in order to account for levels of positive affectivity during the testing situation. PositiveAffectj is a measure of the positive affect of person j assessed just prior to the achievement test.
A comparison of the results of the two analyses is instructive. The two Test Characteristic Curves (TCCs, Test Response Functions, TRFs, Figure 1) are drawn relative to the apparent difficulty of Spelling item 7. So, someone whose estimated ability is the same as the difficulty of item 7 (theta = 0) has an expected score of 4.2 (out of 7) in the first, unadjusted, analysis, but 3.5 in the second, adjusted, analysis. The effect of positive affect has been to raise the expected score by about 0.7 score-points, equivalent to a theta advance of 0.6 logits, a half-year growth in many educational settings.
The slopes of the TCCs are the Test Information Functions (TIFs). These are off-set by about 0.6 logits (as we would predict). The standard errors of the ability- estimate measurements (SEMs, Figure 3) are the inverse square-roots of the TIF. For most purposes, we would like the SEMs to be approximately uniform, giving equal measurement precision across the ability distribution. Here, this would require flatter TIFs, and more uniform distribution of the difficulties of the 7 items across the target range of abilities. This change would also lessen the impact of the affective bias on measurement precision.
Characteristics such as motivation, emotions, fatigue, and other situational factors can be systematic sources of bias and so can lead to estimates that deviate markedly from the actual abilities of the persons on the intended latent variable. The moral of our story is that care should be taken to watch for, and then adjust for, sources of bias in our measures.
Georgios D. Sideridis
Ioannis Tsaousis
University of Crete

Figure 1. Test Characteristic Curves for both analyses
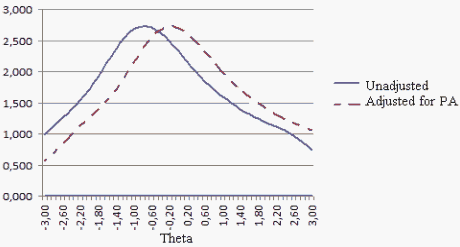
Figure 2. Test Information Functions for both analyses
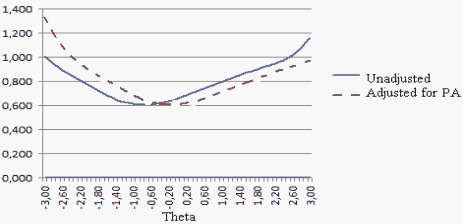
Figure 3. Conditional SEM functions for both analyses
How Much Do Emotions Alter Our Measurements?, Georgios D. Sideridis ... Rasch Measurement Transactions, 2011, 251:1, 1315-6
| Forum | Rasch Measurement Forum to discuss any Rasch-related topic |
Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement
Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.
| Coming Rasch-related Events | |
|---|---|
| Jan. 16 - Feb. 13, 2025, Fri.-Fri. | On-line workshop: Rasch Measurement - Core Topics (E. Smith, Winsteps), www.statistics.com |
| Apr. 8 - Apr. 11, 2026, Wed.-Sat. | National Council for Measurement in Education - Los Angeles, CA, ncme.org/events/2026-annual-meeting |
| Apr. 8 - Apr. 12, 2026, Wed.-Sun. | American Educational Research Association - Los Angeles, CA, www.aera.net/AERA2026 |
| May. 15 - June 12, 2026, Fri.-Fri. | On-line workshop: Rasch Measurement - Core Topics (E. Smith, Winsteps), www.statistics.com |
| June 19 - July 25, 2026, Fri.-Sat. | On-line workshop: Rasch Measurement - Further Topics (E. Smith, Winsteps), www.statistics.com |
The URL of this page is www.rasch.org/rmt/rmt251a.htm
Website: www.rasch.org/rmt/contents.htm