More about Critical Eigenvalue Sizes (Variances) in Standardized-Residual Principal Components Analysis (PCA)

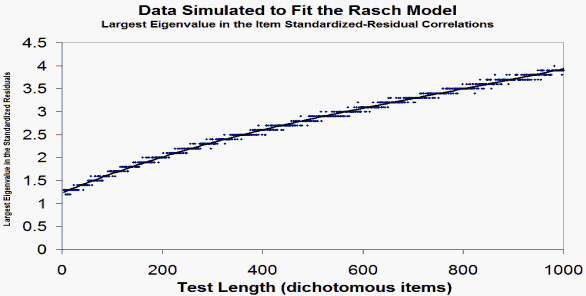
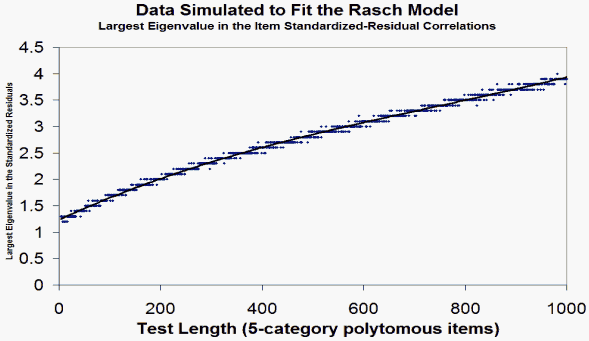
Gilles Raîche in RMT 19:1 p. 102 reports eigenvalues in the range 1.4 to 2.1 for the first component in a PCA of inter-item correlations of standardized residuals of Rasch-fitting data. Test lengths were in the range 20 to 60 items.

Here those findings are extended to dichotomous and polytomous data with test lengths from 3 to 1000 items. The generating person sample of 1000 persons has a normal distribution with a mean of 0 logits and a standard deviation of 2 logits. The generating item distribution is uniform from -2 to +2 logits. For the 5-category polytomous data, the generating Rasch-Andrich thresholds are: -2.53, -0.35, 0.56, 2.32 logits. The Figures shows the eigenvalues sizes of the first components (contrasts) in a PCA of the standardized-residual item-correlation matrices.

For the dichotomous simulations, the eigenvalue increases from 1.3 for 3 items to 4.0 for 1000 items. For 5-category polytomous items, the eigenvalues have the same range.

John Michael Linacre

"Monte Carlo PCA for Parallel Analysis" is Marley Watkins' free software for performing this type of investigation using simulated random-normal deviates, which standardized residuals approximate. For 200 items (variables) and 1000 persons (subjects), that software reports that the first PCA component in the random-normal deviates has an eigenvalue of 2.05 which accords with the findings above.

Alan Tennant

1. PCA: Data Variance: Explained, Modeled and Empirical
2. Critical Eigenvalue Sizes (Variances) in Standardized Residual Principal Components Analysis (PCA)
3. More about Critical Eigenvalue Sizes (Variances) in Standardized-Residual Principal Components Analysis (PCA)
4. Data Variance Explained by Rasch Measures
5. PCA: Variance in Data Explained by Rasch Measures

Linacre J.M., Tennant A. (2009) More about Critical Eigenvalue Sizes (Variances) in Standardized-Residual Principal Components Analysis (PCA), Rasch Measurement Transactions, 2009, 23:3, 1228

Rasch Publications
Rasch Measurement Transactions (free, online)	Rasch Measurement research papers (free, online)	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Applying the Rasch Model 3rd. Ed., Bond & Fox	Best Test Design, Wright & Stone
Rating Scale Analysis, Wright & Masters	Introduction to Rasch Measurement, E. Smith & R. Smith	Introduction to Many-Facet Rasch Measurement, Thomas Eckes	Invariant Measurement: Using Rasch Models in the Social, Behavioral, and Health Sciences, George Engelhard, Jr.	Statistical Analyses for Language Testers, Rita Green
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Journal of Applied Measurement	Rasch models for measurement, David Andrich	Constructing Measures, Mark Wilson	Rasch Analysis in the Human Sciences, Boone, Stave, Yale
in Spanish:	Análisis de Rasch para todos, Agustín Tristán		Mediciones, Posicionamientos y Diagnósticos Competitivos, Juan Ramón Oreja Rodríguez

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt233f.htm

Website: www.rasch.org/rmt/contents.htm