Crossing Person Response Functions

The substantive interpretation of crossing item response functions (IRFs) is fairly well-known. For example, Wright (1997) clearly illustrates how crossing IRFs create a differential ordering of items by difficulty below and above the intersection points. What has not been as clearly realized, despite Wright's valiant efforts in 1992, is that crossing person response functions (PRFs) also cause problems with the substantive interpretation of person performance. The ordering of persons below and above the intersection points varies when PRFs cross. The purpose of this note is to illustrate crossing PRFs, and to show the substantive impact of this situation.

Mosier (1940, 1941) is usually cited as one of the first researchers to discuss PRFs, although graphical displays representing PRFs can also be found in the early work of Thorndike, Thurstone, and several other 19th century researchers working in the area of psychophysics. Operating characteristic functions for dichotomous responses have been proposed by Rasch (1960/1980) and Birnbaum (1968). The Rasch Model for dichotomous responses can be written as

[1]

and the Birnbaum Model for dichotomous responses as

[2]

where θ is a parameter specifying the location of person on the latent variable, δ is the difficulty or location of item, a is a discrimination parameter in the Birnbaum model, and c is the lower asymptote of the function in the Birnbaum model. If we select a particular person, such as Person A, then Equations 1 and 2 can be used to define person response functions. The Rasch PRF for Person A is

[3]

while the Birnbaum PRF is:

[4]

It should be noted that c_A is conceptually closer to a real "guessing" parameter in the Birnbaum PRFs, and that α_A represents person sensitivity to a particular subset of items.

Engelhard (in progress) describes five requirements of invariant measurement that must be met to yield useful inferences for measurement in the social, behavioral, and health sciences. These five requirements are

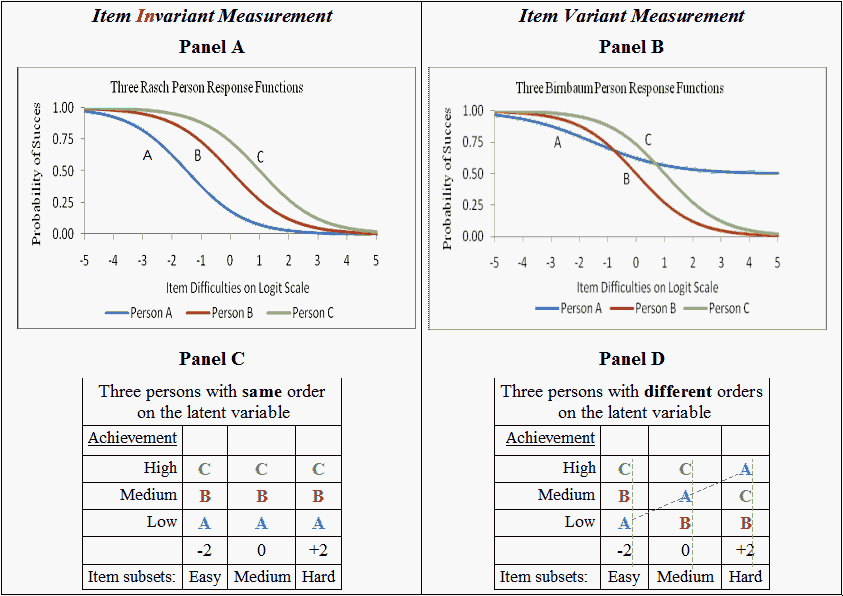
1. The measurement of persons must be independent of the particular items that happen to be used for the measuring: Item-invariant measurement of persons.

2. A more able person must always have a better chance of success on an item than a less able person: non-crossing person response functions.

3. The calibration of the items must be independent of the particular persons used for calibration: Person-invariant calibration of test items.

4. Any person must have a better chance of success on an easy item than on a more difficult item: non-crossing item response functions.

5. Items must be measuring a single underlying latent variable: unidimensionality.

Requirements 1 and 2 address issues related to PRFs.

The Figure illustrates the effects of crossing PRFs. Three PRFs were constructed for two situations: Rasch PRFs that do not cross (Panel A) and Birnbaum PRFs that do cross (Panel B). As shown in Panel C, non-crossing PRFs yield comparable person locations over subsets of items centered around easy items (-2 logits) to hard items (+2 logits). If PRFs do not cross, then Persons A, B, and C are ordered in the same way across item subsets. In other words, item-invariant measurement is achieved with the Rasch model.

Crossing PRFs based on the Birnbaum model (Panel D) yield person ordering that varies as a function of the difficulty of the item subsets. For example, Person A is the lowest achieving person with the lowest probability of success on the easy items, while Person A is the highest achieving person on the hard items. Easy item subsets yield persons ordered as A < B < C, while hard item subsets yield persons ordered B < C < A. In other words, the ordering of persons is not invariant over item subsets with the Birnbaum model.

This note calls attention to the idea that model-data fit can be conceptualized in terms of both IRFs and PRFs (Engelhard, in press). Typically IRFs and differential item functioning analyses are explored. Our work suggests that researchers should also begin to think more systematically about differential person functioning. It is important to recognize the items may function differently over different subgroups of persons (differential item functioning), but it is also important to recognize that persons may not function as intended in their interactions with subsets of test items (differential person functioning).

Aminah Perkins & George Engelhard, Jr.
Emory University, Division of Educational Studies

Birnbaum, A. (1968). Some latent trait models and their use in inferring an examinee's ability, Part 5. In F.M. Lord and M.R. Novick (Eds.), Statistical theories of mental test scores. Reading, MA: Addison-Wesley Publishing Company, Inc.

Engelhard, G. (in progress). Invariant measurement: Rasch models in the social, behavioral, and health sciences. New York: Routledge.

Engelhard, G. (in press: available online). Using item response theory and model-data fit to conceptualize differential item and person functioning for students with disabilities. Educational and Psychological Measurement.

Mosier, C.I. (1940). Psychophysics and mental test theory: Fundamental postulates and elementary theorems. Psychological Review, 47, 355-366.

Mosier, C.I. (1941). Psychophysics and mental test theory. II. The constant process. Psychological Review, 48, 235-249.

Wright, B.D. (1992). IRT in the 1990s: Which Models Work Best? Rasch Measurement Transactions, 6:1, 196-200, www.rasch.org/rmt/rmt61a.htm

Wright, B.D. (1997). A history of social science measurement. Educational Measurement: Issues and Practice, Winter, 33- 45, 52.

---

Perkins A. & Engelhard, G. Jr. (2009) Crossing Person Response Functions, Rasch Measurement Transactions, 2009, 23:1, 1183-4

Rasch Books and Publications
Invariant Measurement: Using Rasch Models in the Social, Behavioral, and Health Sciences, 2nd Edn. George Engelhard, Jr. & Jue Wang	Applying the Rasch Model (Winsteps, Facets) 4th Ed., Bond, Yan, Heene	Advances in Rasch Analyses in the Human Sciences (Winsteps, Facets) 1st Ed., Boone, Staver	Advances in Applications of Rasch Measurement in Science Education, X. Liu & W. J. Boone	Rasch Analysis in the Human Sciences (Winsteps) Boone, Staver, Yale
Introduction to Many-Facet Rasch Measurement (Facets), Thomas Eckes	Statistical Analyses for Language Testers (Facets), Rita Green	Invariant Measurement with Raters and Rating Scales: Rasch Models for Rater-Mediated Assessments (Facets), George Engelhard, Jr. & Stefanie Wind	Aplicação do Modelo de Rasch (Português), de Bond, Trevor G., Fox, Christine M	Appliquer le modèle de Rasch: Défis et pistes de solution (Winsteps) E. Dionne, S. Béland
Exploring Rating Scale Functioning for Survey Research (R, Facets), Stefanie Wind	Rasch Measurement: Applications, Khine	Winsteps Tutorials - free Facets Tutorials - free	Many-Facet Rasch Measurement (Facets) - free, J.M. Linacre	Fairness, Justice and Language Assessment (Winsteps, Facets), McNamara, Knoch, Fan
Other Rasch-Related Resources: Rasch Measurement YouTube Channel
Rasch Measurement Transactions & Rasch Measurement research papers - free	An Introduction to the Rasch Model with Examples in R (eRm, etc.), Debelak, Strobl, Zeigenfuse	Rasch Measurement Theory Analysis in R, Wind, Hua	Applying the Rasch Model in Social Sciences Using R, Lamprianou	El modelo métrico de Rasch: Fundamentación, implementación e interpretación de la medida en ciencias sociales (Spanish Edition), Manuel González-Montesinos M.
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Rasch Models for Measurement, David Andrich	Constructing Measures, Mark Wilson	Best Test Design - free, Wright & Stone Rating Scale Analysis - free, Wright & Masters
Virtual Standard Setting: Setting Cut Scores, Charalambos Kollias	Diseño de Mejores Pruebas - free, Spanish Best Test Design	A Course in Rasch Measurement Theory, Andrich, Marais	Rasch Models in Health, Christensen, Kreiner, Mesba	Multivariate and Mixture Distribution Rasch Models, von Davier, Carstensen

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt231a.htm

Website: www.rasch.org/rmt/contents.htm