Item Discrimination and Rasch-Andrich Thresholds

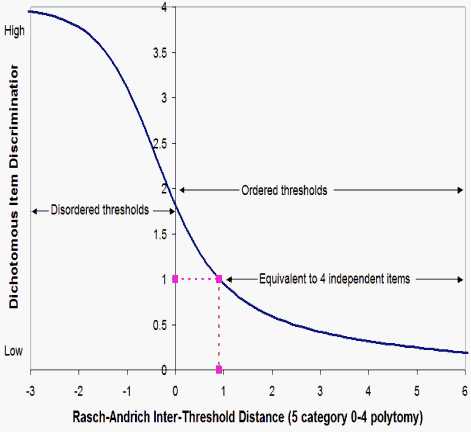
Rasch dichotomous items are modeled to have the same (or known) discrimination. The inter-adjacent-category discrimination of polytomous Rasch items is also modeled to be the same (or known), but the overall discrimination of polytomous items depends on the distance between its Rasch-Andrich thresholds and so can vary across items and instruments..

Consider a five category rating scale, modeled by a set of 4 equally spaced Rasch-Andrich thresholds. Then the overall item discrimination can vary from very steep to almost flat depending on the distance between the threshold values.

The plot shows the relationship between uniform threshold spacing, x, and the item-discrimination slope, a, of an equivalent logistic ogive with the range y = 0-4 score points given by

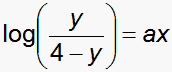A discrimination of a ≥ 1.0 implies that the polytomy is equivalent to summing 4 independent dichotomous 0-1 items. When a = 1.0 the items are of equal difficulty. When the inter-threshold distance is negative, the Rasch-Andrich threshold are "disordered".

It can be seen that one advantage of using Rasch polytomies over independent dichotomous items is that a polytomy can provide higher item discrimination while maintaining the desirable measurement properties of a Rasch model. This is useful for items targeting pass-fail decisions and computer-adaptive testing. This is also one situation in which disordered thresholds can be advantageous.

John Michael Linacre

Item Discrimination and Rasch-Andrich Thresholds, Linacre J.M. Linacre J.M. … Rasch Measurement Transactions, 2006, 20:1 p. 1054

Rasch-Related Resources: Rasch Measurement YouTube Channel
Rasch Measurement Transactions & Rasch Measurement research papers - free	An Introduction to the Rasch Model with Examples in R (eRm, etc.), Debelak, Strobl, Zeigenfuse	Rasch Measurement Theory Analysis in R, Wind, Hua	Applying the Rasch Model in Social Sciences Using R, Lamprianou	El modelo métrico de Rasch: Fundamentación, implementación e interpretación de la medida en ciencias sociales (Spanish Edition), Manuel González-Montesinos M.
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Rasch Models for Measurement, David Andrich	Constructing Measures, Mark Wilson	Best Test Design - free, Wright & Stone Rating Scale Analysis - free, Wright & Masters
Virtual Standard Setting: Setting Cut Scores, Charalambos Kollias	Diseño de Mejores Pruebas - free, Spanish Best Test Design	A Course in Rasch Measurement Theory, Andrich, Marais	Rasch Models in Health, Christensen, Kreiner, Mesba	Multivariate and Mixture Distribution Rasch Models, von Davier, Carstensen
Rasch Books and Publications: Winsteps and Facets
Applying the Rasch Model (Winsteps, Facets) 4th Ed., Bond, Yan, Heene	Advances in Rasch Analyses in the Human Sciences (Winsteps, Facets) 1st Ed., Boone, Staver	Advances in Applications of Rasch Measurement in Science Education, X. Liu & W. J. Boone	Rasch Analysis in the Human Sciences (Winsteps) Boone, Staver, Yale	Appliquer le modèle de Rasch: Défis et pistes de solution (Winsteps) E. Dionne, S. Béland
Introduction to Many-Facet Rasch Measurement (Facets), Thomas Eckes	Rasch Models for Solving Measurement Problems (Facets), George Engelhard, Jr. & Jue Wang	Statistical Analyses for Language Testers (Facets), Rita Green	Invariant Measurement with Raters and Rating Scales: Rasch Models for Rater-Mediated Assessments (Facets), George Engelhard, Jr. & Stefanie Wind	Aplicação do Modelo de Rasch (Português), de Bond, Trevor G., Fox, Christine M
Exploring Rating Scale Functioning for Survey Research (R, Facets), Stefanie Wind	Rasch Measurement: Applications, Khine	Winsteps Tutorials - free Facets Tutorials - free	Many-Facet Rasch Measurement (Facets) - free, J.M. Linacre	Fairness, Justice and Language Assessment (Winsteps, Facets), McNamara, Knoch, Fan

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt201k.htm

Website: www.rasch.org/rmt/contents.htm