Estimating 50% Cumulative Probability (Rasch-Thurstone) Thresholds from Rasch-Andrich thresholds and vice-versa

Rating scale category boundaries can be conceptualized in a number of ways. L. L. Thurstone (1928) describes the computation of .50 cumulative proportions as "scale values." These scale values are now referred to as Thurstone thresholds. They are also the parameters in the "Graded Response" model.

Rasch rating scale structures are parameterized using the points of equal-probability of adjacent categories, rather than the points of equal probability of accumulated category probabilities. Nevertheless, in communicating Rasch findings, it can be convenient to represent Rasch rating scale functioning in terms of Thurstone- type thresholds.

Rasch polytomous models, such as Andrich "rating scale" or Masters "partial credit" models have the form:

1

with the usual notation conventions, and F_g0 = 0. F_gj parameterizes the "Rasch-Andrich threshold" or "step", the point of equal probability of categories j-1 and j. The subscript "g" indicates the manner in which the set of {F_gj} parameters relates to the n or i parameters. For the Andrich "rating scale" model, "g" signifies all items. For the Masters' "Partial Credit" model, "g" signifies item i. For Ben Wright's "Style" model, "g" signifies person n. For an instrument in which different groups of items share common rating scales, "g" identifies the item groups.

Let the Rasch-Thurstone-type thresholds be identified as {T_gj} relative to item difficulty, D_i. Then

2

for j=1,m. So that, multiplying through by the normalizer,

3

Then let

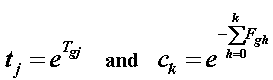
4

so that, for each of j=1,m,

5

If the T_gj are specified, then the t_j are known, and the c_k can be obtained by solving the m simultaneous equations. From the c_k, the F_gh can be computed directly. Thus a polytomous Rasch model can be parameterized in terms of Thurstone-type thresholds using matrix notation and Cramer's rule.

On the other hand, if the F_gh are specified, then the c_k are known. Each of the m equations becomes a polynomial in t_j. The required root always exists. The lower bound of the search for t_j is zero (when the polynomial must be positive), and t_j can be increased until the polynomial becomes negative. When the value of t_j has been found for which the equation is well enough satisfied, then T_gj is computed.

A 3 category, so two threshold, item has Rasch-Andrich thresholds -0.85, 0.85. The lower Rasch-Thurstone-type Threshold is given by j=1:

6

so that t₁ = 0.37, and T₁ is -1.0. By symmetry, T₂ is +1.0.

Working backwards for the Rasch-Andrich thresholds, if the Rasch-Thurstone-type thresholds are -1, +1, then

7

So that F₁ = log_e(1/(e¹ - e^-1)) = -.85, and F₂ = +.85.

John M. Linacre

Thurstone L.L. (1928) Attitudes can be measured. American Journal of Sociology, 33, 529-54.

<

Estimating 50% Cumulative Probability (Rasch-Thurstone) Thresholds. Linacre JM. … Rasch Measurement Transactions, 2003, 16:4 p.901

Rasch Publications
Rasch Measurement Transactions (free, online)	Rasch Measurement research papers (free, online)	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Applying the Rasch Model 3rd. Ed., Bond & Fox	Best Test Design, Wright & Stone
Rating Scale Analysis, Wright & Masters	Introduction to Rasch Measurement, E. Smith & R. Smith	Introduction to Many-Facet Rasch Measurement, Thomas Eckes	Invariant Measurement: Using Rasch Models in the Social, Behavioral, and Health Sciences, George Engelhard, Jr.	Statistical Analyses for Language Testers, Rita Green
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Journal of Applied Measurement	Rasch models for measurement, David Andrich	Constructing Measures, Mark Wilson	Rasch Analysis in the Human Sciences, Boone, Stave, Yale
in Spanish:	Análisis de Rasch para todos, Agustín Tristán		Mediciones, Posicionamientos y Diagnósticos Competitivos, Juan Ramón Oreja Rodríguez

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt164e.htm

Website: www.rasch.org/rmt/contents.htm