Facets, Factors, Elements and Levels

1. Guttman's "Facet" Theory

Early test analysis was based on a simple rectangular conception: people encounter items. This could be termed a "two-facet" situation, loosely borrowing a term from Guttman's (1959) "Facet Theory". From a Rasch perspective, the person's ability, competence, motivation, etc., interacts with the item's difficulty, easiness, challenge, etc., to produce the observed outcome. In order to generalize, the individual persons and items are here termed "elements" of the "person" and "item" facets.

2. The Facets "many-facets" approach

Paired comparisons, such as a Chess Tournament or a Football League, are one-facet situations. The ability of one player interacts directly with the ability of another to produce the outcome. The one facet is "players", and each of its elements is a player. This can be extended easily to a non-rectangular two-facet design in order to estimate the advantage of playing first, e.g., playing the white pieces in Chess. The Rasch model then becomes:

where player n of ability B_n plays the white pieces against player m of ability B_m, and A_w is the advantage of playing white.

A three-facet situation occurs when a person encountering an item is rated by a judge. The person's ability interacting with the item's difficulty is rated by a judge with a degree of leniency or severity. A rating in a high category of a rating scale could equally well result from high ability, low difficulty, or high leniency.

Four-facet situations occur when a person performing a task is rated on items of performance by a judge. For instance, in Occupational Therapy, the person is a patient. The rater is a therapist. The task is "make a sandwich". The item is "find materials".

A typical Rasch model for a four-facet situation is:

where D_i is the difficulty of item i, and F_ik specifies that each item i has its own rating scale structure, i.e., the "partial credit" model.

And so on, for more facets. In these models, no one facet is treated any differently from the others. This is the conceptualization for "Many-facet Rasch Measurement" (Linacre, 1989) and the Facets computer program.

Of course, if all judges are equally severe, then all judge measures will be the same, and they can be omitted from the measurement model without changing the estimates for the other facets. But the inclusion of "dummy" facets, such as equal-severity judges, or gender, age, item type, etc., is often advantageous because their element-level fit statistics are informative.

3. The "Generalizability" approach

Multi-facet data can be conceptualized in other ways. In Generalizability theory, one facet is called the "object of measurement". All other facets are called "facets", and are regarded as sources of unwanted variance. Thus, in G-theory, a rectangular data set is a "one-facet design".

4. The LLTM "Linear Logistic Test Model" approach

In Gerhard Fischer's Linear Logistic Test Model (LLTM), all non-person facets are conceptualized as contributing to item difficulty. So, the dichotomous LLTM model for a four-facet situation (Fischer, 1995) is:

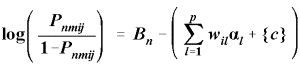
where p is the total count of all item, task and judge elements, and wil identifies which item, task and judge elements interact with person n to produce the current observation. The normalizing constraints are indicated by {c}. In this model, the components of difficulty are termed "factors" instead of "elements", so the model is said to estimate p factors rather than 4 facets. This is because the factors were originally conceptualized as internal components of item design, rather than external elements of item administration. Operationally, this is a two-facet analysis combined with a linear decomposition.

5. The RUMM2020 "Factor" approach

David Andrich's Rasch Unidimensional Measurement Models (RUMM) takes a fourth approach. Here the rater etc. facets are termed "factors" when they are modeled within the person or item facets, and the elements within the factors are termed "levels". Our four-facet model is expressed as a two-facet person-item model, with the item facet defined to encompass three factors. The "rating scale" version is:

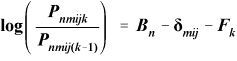
where D_i is an average of all δ_mij for item i, A_m is an average of all δ_mij for task m, etc.

This approach is particularly convenient because it can be applied to the output of any two-facet estimation program, by hand or with a spreadsheet program. Operationally, this is a two-facet analysis followed by a linear decomposition.. Missing δ_mij may need to be imputed. With a fully-crossed design, a robust averaging method is standard-error weighting (RMT 8:3 p. 376). With some extra effort, element-level quality-control fit statistics can also be computed.

John M. Linacre

Fischer, G.H., & Molenaar, I.W. (Eds.) (1995) Rasch Models: Foundations, Recent Developments and Applications. New York: Springer.

Guttman, L. (1959) A structural theory for intergroup beliefs and action. American Sociological Review, 24, 318-328.

Facets, factors, elements and levels. Linacre, JM. … 16:2 p.880

Facets, factors, elements and levels. Linacre, JM. … Rasch Measurement Transactions, 2002, 16:2 p.880

Rasch Publications
Rasch Measurement Transactions (free, online)	Rasch Measurement research papers (free, online)	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Applying the Rasch Model 3rd. Ed., Bond & Fox	Best Test Design, Wright & Stone
Rating Scale Analysis, Wright & Masters	Introduction to Rasch Measurement, E. Smith & R. Smith	Introduction to Many-Facet Rasch Measurement, Thomas Eckes	Invariant Measurement: Using Rasch Models in the Social, Behavioral, and Health Sciences, George Engelhard, Jr.	Statistical Analyses for Language Testers, Rita Green
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Journal of Applied Measurement	Rasch models for measurement, David Andrich	Constructing Measures, Mark Wilson	Rasch Analysis in the Human Sciences, Boone, Stave, Yale
in Spanish:	Análisis de Rasch para todos, Agustín Tristán		Mediciones, Posicionamientos y Diagnósticos Competitivos, Juan Ramón Oreja Rodríguez

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt162h.htm

Website: www.rasch.org/rmt/contents.htm