Immediate Raw Score to Logit Conversion

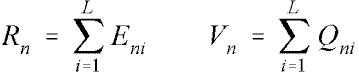
A supposed flaw in the Rasch model can be used to great advantage. Bruce Thompson informs us that Fan (1998) and MacDonald and Paunonen (2002) support his perception that the correlation between Rasch measures and raw scores is always .97 ±.02, i.e., is effectively linear. Malec et al. (2000) report a correlation of .98 for their clinical data. If this also holds true for your data then you can immediately convert raw scores to logits!

What conditions must hold for this hold true?
(a) The raw scores must all be on the same set of items.
(b) The proportion of very high and very low scores is low.

Then we have these convenient relationships. For each person n and item i of a test of length L, there is an observation X_ni. Its Rasch model expectation is E_ni, and the modeled variance of the observation around its expectation is Q_ni (see Wright and Masters, 1982, p. 100). Thus, person n's raw score, R_n, and raw score "error" variance, V_n , are given by:

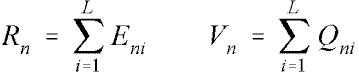
An approximate conversion factor between raw scores and logits for person n of ability B_n, at the center of the test characteristic curve is the slope of the curve: 1/V_n.

Suppose we know the observed standard deviation, S, of the raw scores of a sample on a test and the reliability estimate (KR-20, Cronbach Alpha) of the test for the same sample, R. Then, from the definition of Reliability as "True Variance" / "Observed Variance", raw score error variance = S²(1-R). So that the raw-score-to-Rasch-measure conversion factor is 1/(S²(1-R)) .

It is conventional to set the origin of the logit scale in the center of the test, i.e., where the raw score is about 50%. This gives the convenient raw score-to-measure conversion:

B_n = (R_n - (Maximum score + Minimum score)/2 ) / S²(1-R)

And the standard error of B_n is 1/sqrt(V_n) = 1/(S sqrt(1-R)) logits.

Applying this to the Wright & Masters (1982) "Liking for Science" data: Raw score S.D. = 8.6, Reliability = .87, minimum score = 0, maximum score = 50. Measure for raw score of 20 = -0.52, for 30 = 0.52, with S.E. ±.32. Winsteps says -0.55, 0.61 with S.E. ±.34. So that the results are statistically equivalent.

John M. Linacre

Fan, X. (1998) Item Response Theory and classical test theory (CTT): An empirical comparison of their item/person statistics. Educational and Psychological Measurement, 58, 357-381.

MacDonald, P., & Paunonen, S.V. (2002) A Monte Carlo comparison of item and person statistics based on item response theory versus classical test theory. Educational and Psychological Measurement, 62.

Malec J. F., Moessner, A. M., Kragness, M., and Lezak, M.D. (2000) Refining a measure of brain injury sequelae to predict postacute rehabilitation outcome: rating scale analysis of the Mayo-Portland Adaptability Inventory (MPAI). Journal of Head Trauma Rehabilitation, 15 (1), 670-682.

Immediate raw score to logit conversion. Linacre, JM. … 16:2 p.877

Immediate raw score to logit conversion. Linacre, JM. … Rasch Measurement Transactions, 2002, 16:2 p.877

Rasch Books and Publications
Invariant Measurement: Using Rasch Models in the Social, Behavioral, and Health Sciences, 2nd Edn. George Engelhard, Jr. & Jue Wang	Applying the Rasch Model (Winsteps, Facets) 4th Ed., Bond, Yan, Heene	Advances in Rasch Analyses in the Human Sciences (Winsteps, Facets) 1st Ed., Boone, Staver	Advances in Applications of Rasch Measurement in Science Education, X. Liu & W. J. Boone	Rasch Analysis in the Human Sciences (Winsteps) Boone, Staver, Yale
Introduction to Many-Facet Rasch Measurement (Facets), Thomas Eckes	Statistical Analyses for Language Testers (Facets), Rita Green	Invariant Measurement with Raters and Rating Scales: Rasch Models for Rater-Mediated Assessments (Facets), George Engelhard, Jr. & Stefanie Wind	Aplicação do Modelo de Rasch (Português), de Bond, Trevor G., Fox, Christine M	Appliquer le modèle de Rasch: Défis et pistes de solution (Winsteps) E. Dionne, S. Béland
Exploring Rating Scale Functioning for Survey Research (R, Facets), Stefanie Wind	Rasch Measurement: Applications, Khine	Winsteps Tutorials - free Facets Tutorials - free	Many-Facet Rasch Measurement (Facets) - free, J.M. Linacre	Fairness, Justice and Language Assessment (Winsteps, Facets), McNamara, Knoch, Fan
Other Rasch-Related Resources: Rasch Measurement YouTube Channel
Rasch Measurement Transactions & Rasch Measurement research papers - free	An Introduction to the Rasch Model with Examples in R (eRm, etc.), Debelak, Strobl, Zeigenfuse	Rasch Measurement Theory Analysis in R, Wind, Hua	Applying the Rasch Model in Social Sciences Using R, Lamprianou	El modelo métrico de Rasch: Fundamentación, implementación e interpretación de la medida en ciencias sociales (Spanish Edition), Manuel González-Montesinos M.
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Rasch Models for Measurement, David Andrich	Constructing Measures, Mark Wilson	Best Test Design - free, Wright & Stone Rating Scale Analysis - free, Wright & Masters
Virtual Standard Setting: Setting Cut Scores, Charalambos Kollias	Diseño de Mejores Pruebas - free, Spanish Best Test Design	A Course in Rasch Measurement Theory, Andrich, Marais	Rasch Models in Health, Christensen, Kreiner, Mesba	Multivariate and Mixture Distribution Rasch Models, von Davier, Carstensen

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt162e.htm

Website: www.rasch.org/rmt/contents.htm