The Hyperbolic Cosine Unfolding Quasi-Rasch Model

The Hyperbolic Cosine Model (HCM, Andrich & Luo, 1993) for dichotomous unfolding responses is derived from the Rasch model for 3-ordered-category responses, but is not, itself, a Rasch model. Consider a dichotomous preference item: "I owe a lot to my parents" (Agree/Disagree). The meaning of Agree seems obvious. But what does Disagree mean? I owe little to my parents? I owe everything to my parents? Thus, in constructing the HCM, the Disagree response is resolved into two latent components. One component is, Disagree below, "I owe a little ..." The other is Disagree above, "I owe everything ..."

A Rasch model for three ordered categories is:

where k=0 is "Disagree below", k=1 is "Agree", and k=2 is "Disagree above", and ΣF_ik=0. The HCM function for a Disagree response, P_niD, is the sum of the probabilities of the "Disagree below" and "Disagree above" categories. The Agree category remains as P_niA. Summing,

A convenient identity for the hyperbolic cosine is:

So that, after reparameterization (Andrich, 1996; Luo, 1998), the HCM can be expressed more elegantly as:

where

It is seen that P_niA = P_niD = 0.5 when ρ_i = B_n - D_i or, because cosh(x) = cosh(-x), when -ρ_i = B_n - D_i . Thus the new parameter, ρ_i, is half the distance between the two crossing points of the Agree and Disagree response curves. This characterizes the latitude of acceptance, an important concept in attitude measurement. Note that this model requires that the probability of observing Agree reach .5 at some point along the latent variable. The Figure shows the HCM functions and the corresponding Rasch model for 3 categories (in dotted lines).

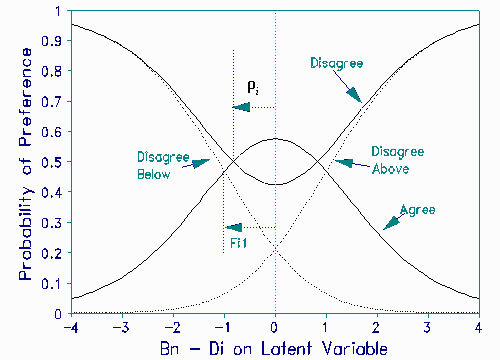
Why is HCM not a Rasch model? Rasch models require parameter separability or, in statistical terms, sufficient statistics. HCM does not have these.

Choosing a Response Model

If the data follow the Rasch (or other cumulative) model, responses are positively correlated across items. If the data follow the HCM (or other unfolding model), an item has positive correlations with nearby items, but negative correlations with distant items. The HCM equation has been expanded into a general form for dichotomous unfolding responses (Luo, 1998), and then into a general form for polytomous unfolding responses (Luo, 2001).

Guanzhong Luo, Murdoch University, Australia

Andrich, D. (1996). A hyperbolic cosine latent trait model for unfolding polytomous responses: reconciling Thurstone and Likert methodologies. British Journal of Mathematical and Statistical Psychology, 49, 347-365.

Andrich, D. & Luo, G. (1993). A hyperbolic cosine latent trait model for unfolding dichotomous single-stimulus responses. Applied Psychological Measurement, 17, 253-276.

Luo, G. (1998). A general formulation of unidimensional unfolding and pairwise preference models: making explicit the latitude of acceptance. Journal of Mathematical Psychology. 42, 400-417.

Luo, G. (2001). A class of probabilistic unfolding models for polytomous responses. Journal of Mathematical Psychology. 45, 224-248.

Hyperbolic cosine unfolding quasi-Rasch model. Luo G. … 16:1 p.870

Hyperbolic cosine unfolding quasi-Rasch model. Luo G. … Rasch Measurement Transactions, 2002, 16:1 p.870

Rasch Books and Publications
Invariant Measurement: Using Rasch Models in the Social, Behavioral, and Health Sciences, 2nd Edn. George Engelhard, Jr. & Jue Wang	Applying the Rasch Model (Winsteps, Facets) 4th Ed., Bond, Yan, Heene	Advances in Rasch Analyses in the Human Sciences (Winsteps, Facets) 1st Ed., Boone, Staver	Advances in Applications of Rasch Measurement in Science Education, X. Liu & W. J. Boone	Rasch Analysis in the Human Sciences (Winsteps) Boone, Staver, Yale
Introduction to Many-Facet Rasch Measurement (Facets), Thomas Eckes	Statistical Analyses for Language Testers (Facets), Rita Green	Invariant Measurement with Raters and Rating Scales: Rasch Models for Rater-Mediated Assessments (Facets), George Engelhard, Jr. & Stefanie Wind	Aplicação do Modelo de Rasch (Português), de Bond, Trevor G., Fox, Christine M	Appliquer le modèle de Rasch: Défis et pistes de solution (Winsteps) E. Dionne, S. Béland
Exploring Rating Scale Functioning for Survey Research (R, Facets), Stefanie Wind	Rasch Measurement: Applications, Khine	Winsteps Tutorials - free Facets Tutorials - free	Many-Facet Rasch Measurement (Facets) - free, J.M. Linacre	Fairness, Justice and Language Assessment (Winsteps, Facets), McNamara, Knoch, Fan
Other Rasch-Related Resources: Rasch Measurement YouTube Channel
Rasch Measurement Transactions & Rasch Measurement research papers - free	An Introduction to the Rasch Model with Examples in R (eRm, etc.), Debelak, Strobl, Zeigenfuse	Rasch Measurement Theory Analysis in R, Wind, Hua	Applying the Rasch Model in Social Sciences Using R, Lamprianou	El modelo métrico de Rasch: Fundamentación, implementación e interpretación de la medida en ciencias sociales (Spanish Edition), Manuel González-Montesinos M.
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Rasch Models for Measurement, David Andrich	Constructing Measures, Mark Wilson	Best Test Design - free, Wright & Stone Rating Scale Analysis - free, Wright & Masters
Virtual Standard Setting: Setting Cut Scores, Charalambos Kollias	Diseño de Mejores Pruebas - free, Spanish Best Test Design	A Course in Rasch Measurement Theory, Andrich, Marais	Rasch Models in Health, Christensen, Kreiner, Mesba	Multivariate and Mixture Distribution Rasch Models, von Davier, Carstensen

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt161p.htm

Website: www.rasch.org/rmt/contents.htm