Residuals and Rating Scales

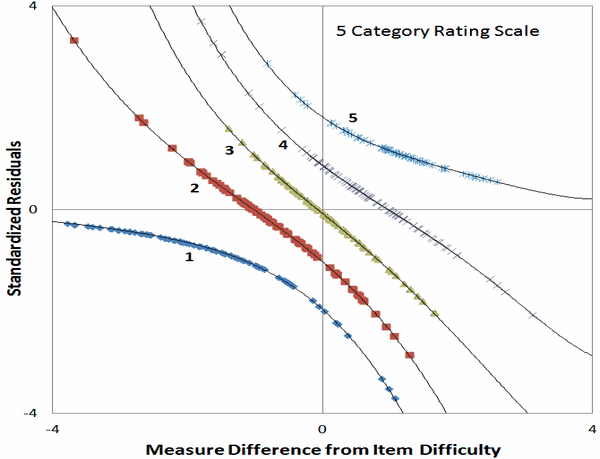
Measures are located on infinite, continuous variables, but they are observed as observations on finite discrete rating (or other) scales. Stephen Humphry (West Australia Writing Assessment, 2002) notices the distinctive patterns of residuals that result.

Figure 1 shows the standardized residuals for observations on a typical 5 category rating scale plotted against measures (relative to the mean difficulty of the item). A residual is the difference between the observation and its expected value for a respondent of a particular ability on that item. The Rasch model also predicts the distribution of observations around their expected value. The residual is divided by the standard deviation of this "model" distribution to obtain the standardized residual.

Each of the distinctive striations in the plot corresponds to the standardized residuals for one of the categories of the rating scale. At each measure, the striations are located at equal vertical intervals, equal in size to the "model" standard deviation. The curvature of the lines is indicative of changes in the item information along the latent variable.

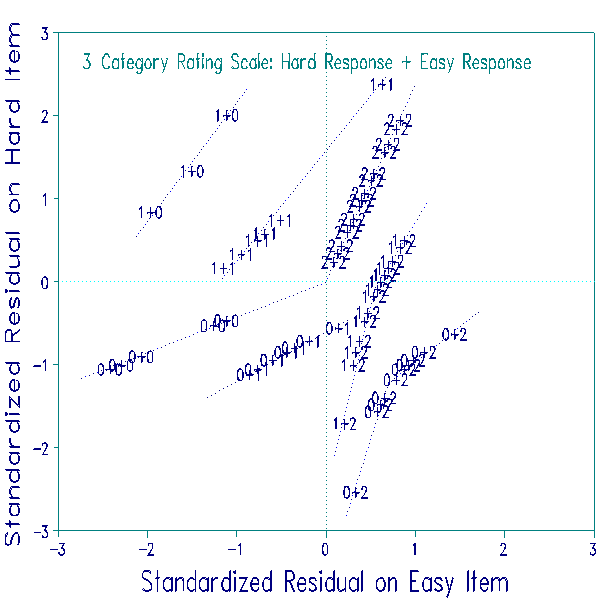
When the standardized residuals for the responses to two items by the same persons are cross- plotted, then distinctive patterns emerge. These are shown in Figure 2. The pairs of responses to the 3- category items are shown on the plot as "response to easy item"+"response to hard item". For each traceline, the lower, left end is generated by high abilities, and the higher, right end by low abilities.

Only 3 instances of the unlikely pairing, "0"+"1" (low rating on the easy item, middle rating on the hard item), are observed. They are in the upper left corner. The most unlikely response pairing, "0"+"2", is not observed here, but would be found in the extreme upper-left corner. The "0"+"0" and "2"+"2" trace lines approach the origin for persons toward the extreme low and extreme high ends, respectively, of the latent variable.

John M. Linacre

Residuals and rating scales. Humphry S. … 16:1 p.866

Residuals and rating scales. Humphry S. … Rasch Measurement Transactions, 2002, 16:1 p.866

Rasch Books and Publications
Invariant Measurement: Using Rasch Models in the Social, Behavioral, and Health Sciences, 2nd Edn. George Engelhard, Jr. & Jue Wang	Applying the Rasch Model (Winsteps, Facets) 4th Ed., Bond, Yan, Heene	Advances in Rasch Analyses in the Human Sciences (Winsteps, Facets) 1st Ed., Boone, Staver	Advances in Applications of Rasch Measurement in Science Education, X. Liu & W. J. Boone	Rasch Analysis in the Human Sciences (Winsteps) Boone, Staver, Yale
Introduction to Many-Facet Rasch Measurement (Facets), Thomas Eckes	Statistical Analyses for Language Testers (Facets), Rita Green	Invariant Measurement with Raters and Rating Scales: Rasch Models for Rater-Mediated Assessments (Facets), George Engelhard, Jr. & Stefanie Wind	Aplicação do Modelo de Rasch (Português), de Bond, Trevor G., Fox, Christine M	Appliquer le modèle de Rasch: Défis et pistes de solution (Winsteps) E. Dionne, S. Béland
Exploring Rating Scale Functioning for Survey Research (R, Facets), Stefanie Wind	Rasch Measurement: Applications, Khine	Winsteps Tutorials - free Facets Tutorials - free	Many-Facet Rasch Measurement (Facets) - free, J.M. Linacre	Fairness, Justice and Language Assessment (Winsteps, Facets), McNamara, Knoch, Fan
Other Rasch-Related Resources: Rasch Measurement YouTube Channel
Rasch Measurement Transactions & Rasch Measurement research papers - free	An Introduction to the Rasch Model with Examples in R (eRm, etc.), Debelak, Strobl, Zeigenfuse	Rasch Measurement Theory Analysis in R, Wind, Hua	Applying the Rasch Model in Social Sciences Using R, Lamprianou	El modelo métrico de Rasch: Fundamentación, implementación e interpretación de la medida en ciencias sociales (Spanish Edition), Manuel González-Montesinos M.
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Rasch Models for Measurement, David Andrich	Constructing Measures, Mark Wilson	Best Test Design - free, Wright & Stone Rating Scale Analysis - free, Wright & Masters
Virtual Standard Setting: Setting Cut Scores, Charalambos Kollias	Diseño de Mejores Pruebas - free, Spanish Best Test Design	A Course in Rasch Measurement Theory, Andrich, Marais	Rasch Models in Health, Christensen, Kreiner, Mesba	Multivariate and Mixture Distribution Rasch Models, von Davier, Carstensen

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt161j.htm

Website: www.rasch.org/rmt/contents.htm