Scores and Measures

"Obviously, most psychometricians would favor a less straightforward sense of representation, one in which sameness or difference of test scores only indicated sameness or difference of the attribute represented with a specific probability. For example, Rasch's theory of test scores, mentioned in Chapter 1, allows people of the same ability to obtain different scores and people of different levels of ability to get the same score on particular occasions."

Joel Michell (1999) Measurement in Psychology: Critical History of a Methodological Concept. Cambridge: Cambridge University Press. p. 166-7 n.

Can anyone illuminate what he might be after here?

Trevor Bond

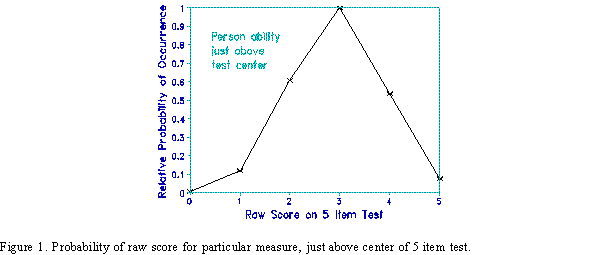
Michell is contrasting Rasch models with "error-free" models. In these strictly deterministic models, a latent measure is always observed as a particular score, and a particular score always indicates the same latent measure. Under Rasch model conditions, in contrast, the relationship between measures and scores is probabilistic. Any score can be observed for a particular measure, and any measure can generate a particular score. Figures 1 and 2 illustrate this for a test of 5 uniformly distributed items.

Michell, however, errs when he perceives the Rasch model to be a model of psychological processes, rather than the necessary and sufficient expression of measurement. "If Rasch's hypothesis is correct, the estimates can be regarded as measures of the ability involved. Some psychologists claim to be able in this way to measure intellectual abilities." (p. 12)

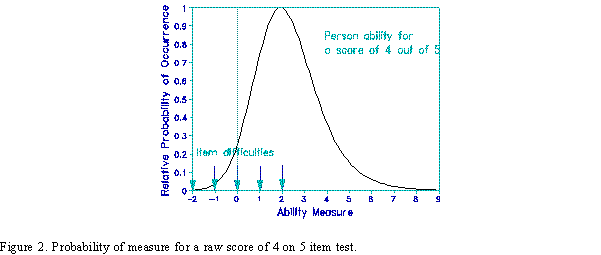
Scores and measures. Michell J, Bond T. … Rasch Measurement Transactions, 2000, 14:1 p.731

Rasch Publications
Rasch Measurement Transactions (free, online)	Rasch Measurement research papers (free, online)	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Applying the Rasch Model 3rd. Ed., Bond & Fox	Best Test Design, Wright & Stone
Rating Scale Analysis, Wright & Masters	Introduction to Rasch Measurement, E. Smith & R. Smith	Introduction to Many-Facet Rasch Measurement, Thomas Eckes	Invariant Measurement: Using Rasch Models in the Social, Behavioral, and Health Sciences, George Engelhard, Jr.	Statistical Analyses for Language Testers, Rita Green
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Journal of Applied Measurement	Rasch models for measurement, David Andrich	Constructing Measures, Mark Wilson	Rasch Analysis in the Human Sciences, Boone, Stave, Yale
in Spanish:	Análisis de Rasch para todos, Agustín Tristán		Mediciones, Posicionamientos y Diagnósticos Competitivos, Juan Ramón Oreja Rodríguez

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt141b.htm

Website: www.rasch.org/rmt/contents.htm