Does Rasch Construct Bad Rulers?

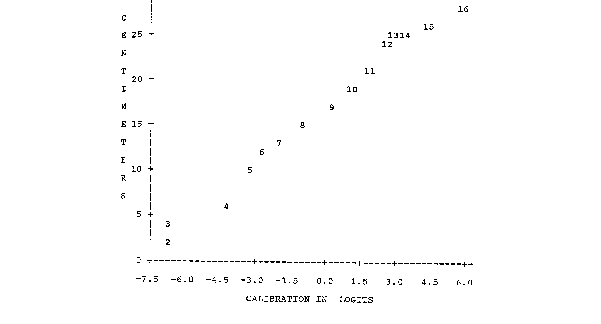
"My attempt to measure physical length using Rasch measurement did not recover the linearity of the underlying physical measurement. From this, it seems to me that Rasch measurement alone is not sufficient for scientific investigation of phenomena. It is merely the production of a locally linear measurement scale. For example, I can scale anxiety items quite nicely - but what is it that I am measuring? My explanation is limited to the content of these items. Unless there is an isomorphic linkage between a Rasch unit and a universal, substantively meaningful unit (such as the meter), then you will never be able to generate Rasch measurement of any variable that is not specific to a culture or some other subset or subdivision of humans."
Paul Barrett, Liverpool University

Ben Wright, U. of Chicago, responds
May I congratulate you for attempting an experiment which I have encouraged many others to perform? As I learned in my days as a research assistant to Nobel physicist Robert Mulliken, there are hundreds of ways an experiment can go wrong, but only one way it can go right. Have you traveled down that one right way or one of those many wrong ones? The history of science is strewn with confusing and contradictory experimental results. The search for the Top Quark involved thousands of experimental failures, and yet no one now doubts that the Top Quark exists. "No isolated experiment, however significant in itself, can suffice for the experimental demonstration of any natural phenomenon." (R.A. Fisher, 1935). Since physical variables have been recovered from Rasch analyses of known objects so many different times (e.g., distance in RMT 7:1 p. 268, weight in 11:2 p. 557), your experiment will need a lot more substance and corroboration before it can be considered a serious challenge to the fundamental linearity and scientific standing of Rasch measures.

William P. Fisher, Jr, Louisiana SU Medical Center, responds
Thank you for providing an opportunity to elaborate on this important topic. The core issue is in this statement: "My explanation is limited to the content of these items." This implies that the linearity of Rasch measures is restricted to the specific items included in the scaling. But, on the contrary, insofar as you've achieved the Rasch ideal of parameter separation and specific objectivity, you've established that this particular sample of items is representative of the population of all possible similar articulations of the variable. Your explanation is no more tied to these particular items' contents than the explanation of any variable, metaphor, or shared linguistic concept is dependent on the particular instruments or words that mediate its expression.

You have, however, discovered a conundrum. An experiment intended to recover physical length has, instead, constructed some type of psychological length. We are well aware that physical time and psychological time are not isomorphic. At times of stress, time can seem to stand still. The relationship between physical and psychological length is less clear. You have the opportunity to deepen your investigation into psychological length. You can also recast your experiment and try again to recover physical measures. Since the ideal of perfect concatenation forms the basis of physical measurement of length (RMT 11:2 p. 558) and of Rasch measurement (RMT 2:1 p. 16), they are, in fact, equally immune to invalidation by experiment.

From a broader perspective, however, all measures, physical, chemical, or otherwise, are specific to culture! Insofar as Western science has spread around the globe, it is the scientific culture through which measures generalize (Margolis, 1993). Measures do not exist in nature, and it is not things "in themselves" that are understood or explained. Rather, measures and quantitative relationships are artifacts of technology and require persons trained in reading, creating, and maintaining that technology to have any impact.

The scientific culture is a network of scientists and technicians who 1) have seen their independent experiments repeatedly converge on the same variable across instruments, samples, observers, etc., producing a commonality that works as an agent of agreement and standardization; and who, because of these converging observations, 2) have gotten together to routinize that commonality in a standard format as a universal metric.

As O'Connell (1993) points out, scientific entities are not universal until people who care about them make them so. Universal metrics have never been created for any variable by "discovering" them already existing in nature. Rather, measures generalize around the globe only to the extent that laboratory work is condensed into a portable technology that reproduces laboratory conditions anywhere. A single researcher might well manage to simultaneously invent and discover a new and generalizable variable, but his or her metric will become the standard only to the extent that it is reproduced by others and agreed upon by them for use. Universal metrics are as much social phenomena as natural.

With conjoint measurement models, the psychosocial sciences are, for the first time, obtaining some convergence of independent experiments. The next step in the struggle for generalizable scientific quantification is the formation of the crucial metrological networks through which reference-standard instruments and samples are circulated, and so used to maintain the uniform metric standard. It is at this point that Rasch measures will become truly scientific.

Fisher R.A. (1935) The design of experiments. New York: Hafner.

Margolis H. (1993). Paradigms and barriers: How habits of mind govern scientific beliefs. Chicago: University of Chicago Press.

O'Connell J. (1993). Metrology: The creation of universality by the circulation of particulars. Social Studies of Science, 23, 129-173.

"In order to be able to demonstrate to my opponents the truth of my conclusions, I have been forced to prove them by a variety of experiments; though to satisfy my own mind alone, I have never felt it necessary to make any."

Galileo Galilei (1564-1642), quoted in Burtt E.A. (1932) The metaphysical foundations of modern science. Garden City NY: Doubleday Anchor, p.76.

Does Rasch Construct Bad Rulers? Barrett P., Wright B.D., Fisher W.P. Jr. … Rasch Measurement Transactions, 1999, 12:4 p.

Rasch Books and Publications
Invariant Measurement: Using Rasch Models in the Social, Behavioral, and Health Sciences, 2nd Edn. George Engelhard, Jr. & Jue Wang	Applying the Rasch Model (Winsteps, Facets) 4th Ed., Bond, Yan, Heene	Advances in Rasch Analyses in the Human Sciences (Winsteps, Facets) 1st Ed., Boone, Staver	Advances in Applications of Rasch Measurement in Science Education, X. Liu & W. J. Boone	Rasch Analysis in the Human Sciences (Winsteps) Boone, Staver, Yale
Introduction to Many-Facet Rasch Measurement (Facets), Thomas Eckes	Statistical Analyses for Language Testers (Facets), Rita Green	Invariant Measurement with Raters and Rating Scales: Rasch Models for Rater-Mediated Assessments (Facets), George Engelhard, Jr. & Stefanie Wind	Aplicação do Modelo de Rasch (Português), de Bond, Trevor G., Fox, Christine M	Appliquer le modèle de Rasch: Défis et pistes de solution (Winsteps) E. Dionne, S. Béland
Exploring Rating Scale Functioning for Survey Research (R, Facets), Stefanie Wind	Rasch Measurement: Applications, Khine	Winsteps Tutorials - free Facets Tutorials - free	Many-Facet Rasch Measurement (Facets) - free, J.M. Linacre	Fairness, Justice and Language Assessment (Winsteps, Facets), McNamara, Knoch, Fan
Other Rasch-Related Resources: Rasch Measurement YouTube Channel
Rasch Measurement Transactions & Rasch Measurement research papers - free	An Introduction to the Rasch Model with Examples in R (eRm, etc.), Debelak, Strobl, Zeigenfuse	Rasch Measurement Theory Analysis in R, Wind, Hua	Applying the Rasch Model in Social Sciences Using R, Lamprianou	El modelo métrico de Rasch: Fundamentación, implementación e interpretación de la medida en ciencias sociales (Spanish Edition), Manuel González-Montesinos M.
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Rasch Models for Measurement, David Andrich	Constructing Measures, Mark Wilson	Best Test Design - free, Wright & Stone Rating Scale Analysis - free, Wright & Masters
Virtual Standard Setting: Setting Cut Scores, Charalambos Kollias	Diseño de Mejores Pruebas - free, Spanish Best Test Design	A Course in Rasch Measurement Theory, Andrich, Marais	Rasch Models in Health, Christensen, Kreiner, Mesba	Multivariate and Mixture Distribution Rasch Models, von Davier, Carstensen

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt124a.htm

Website: www.rasch.org/rmt/contents.htm