The Normal Cumulative Distribution Function
and the Logistic Ogive

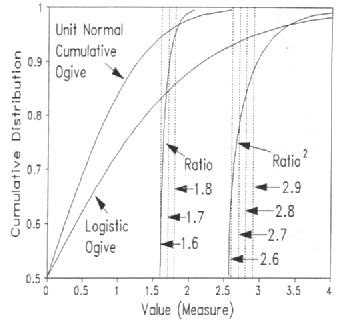
There is a convenient arithmetical relationship between the unit normal ogive and the logistic ogive. Berkson (1944) takes advantage of it for bio-assay calculations. Cohen (1979; Wright & Stone, 1979) use it to simplify the estimation of Rasch measures with the PROX algorithm. The standard relationship is specified as:

where Ψ is the logistic function (in logits) and Φ is the normal cumulative function (in probits). The standard equating value of 1.7 minimizes the maximum difference between the functions (Camilli, 1994). [1 logit ≈ 1.7 probits]

Measures estimated with the PROX algorithm are, at times, too central. The Figure depicts the exact relationship for the upper halves of the ogives. The lower halves follow the same pattern. Close to the center, y=0.52, the logistic ogive is about 1.6 times further away from the y-axis than the normal ogive. The ratio is 1.65 at y=0.80, then 1.70 at y=0.88, and 1.80 at y=0.96. Thus 1.7 is too high unless the average success rate (p-value) exceeds 85%.

For PROX, the variance divisor is the ratio squared. For practical applications where the expected success rate is over 70%, a useful value of Ratio² is 2.65 (instead of 2.89), together with Ratio⁴ of 7.0 (instead of 8.35, Wright & Stone, 1978, p.40).

John M. Linacre

Berkson J. 1944. Applications of the logistic function to bio-assay. Journal of the American Statistical Society 39, 357-365

Camilli G. 1994. Origin of the scaling constant d=1.7, in item response theory. Journal of Educational and Behavioral Statistics 19:3, 293-5

Cohen L. 1979. Approximate expressions for parameter estimates in the Rasch model. British Journal of Mathematical and Statistical Psychology 32:1, 13-120

Wright BD, Stone MH. 1979. Best Test Design. Chicago IL: MESA Press

The Normal Cumulative Distribution Function and the Logistic Ogive: Probit and Logit. Linacre J. M. … Rasch Measurement Transactions, 1997, 11:2 p. 569.

Rasch Publications
Rasch Measurement Transactions (free, online)	Rasch Measurement research papers (free, online)	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Applying the Rasch Model 3rd. Ed., Bond & Fox	Best Test Design, Wright & Stone
Rating Scale Analysis, Wright & Masters	Introduction to Rasch Measurement, E. Smith & R. Smith	Introduction to Many-Facet Rasch Measurement, Thomas Eckes	Invariant Measurement: Using Rasch Models in the Social, Behavioral, and Health Sciences, George Engelhard, Jr.	Statistical Analyses for Language Testers, Rita Green
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Journal of Applied Measurement	Rasch models for measurement, David Andrich	Constructing Measures, Mark Wilson	Rasch Analysis in the Human Sciences, Boone, Stave, Yale
in Spanish:	Análisis de Rasch para todos, Agustín Tristán		Mediciones, Posicionamientos y Diagnósticos Competitivos, Juan Ramón Oreja Rodríguez

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt112m.htm

Website: www.rasch.org/rmt/contents.htm