Score Inflation due to Examinee Control of a Stopping Rule
Examinees like methods that improve their results without
improving their performance. I tried one method myself on a recent
administration of the Graduate Record Examination (GRE).
The GRE was computer-administered with the instruction that a
minimum number of items must be answered. After that, the examinee
could stop answering items at any point and let the time allotted
for the examination run out. I tried a strategy identified by
Slater and Schaeffer (1996):
After the minimum number of items have been answered, continue to
answer items until you are fairly certain you will get the item on
your computer screen wrong. Do not answer that item and let time
expire.
This strategy is intended to increase the number of correct
answers while holding the number of incorrect answers constant.
Since an examinee's estimated measure is
Reported measure =
loge(Right/Wrong) + Average Item Difficulty,
increasing the number of right answers increases the measure.
Avoiding wrong answers prevents the measure from decreasing. This
is called the Numerator Inflation Strategy (NIS). Does it
work?
I took real response strings from a fixed-length 90 item CAT
administration and implemented NIS perfectly with
different minimum item response requirements. I truncated each
response string just before the first wrong answer after the
minimum number of responses. This produced two measures, one for
the truncated string and one for the whole string. The Figure
summarizes the results.
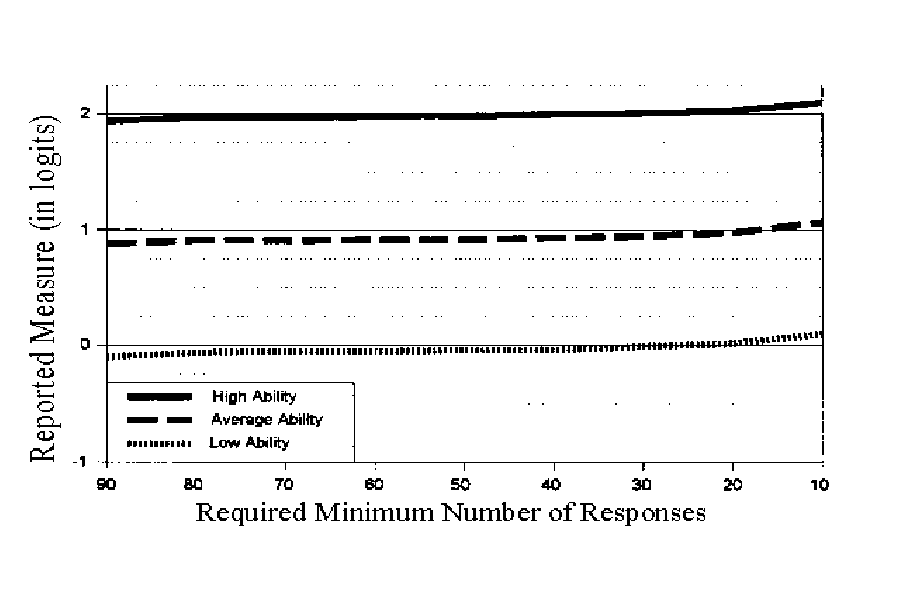In the Figure, three representative performance levels are
shown. Measures for those levels are at 0, 1 and 2 logits. The
slightly sloped lines are average NIS measures for each of the
three levels. In this example, when the minimum number of items
required is very low (right side of Figure), and you know what you
are doing, then you can, on average, raise your reported
measure by about .1 logits above your overall measure. But when
the minimum number of items is high (left side of Figure), then, on
average, you will lower your reported measure by about .1
logits. The reason for these results is that avoiding a wrong
answer on a short test raises your measure by minimizing the
denominator of wrong answers. But on a long test, stopping just
before the first wrong answer penalizes you because you no longer
have the opportunity to improve your measure with a subsequent run
of right answers.
In my case, employing the NIS strategy probably did me no good
and may even have lowered my reported measure. But, for the
marginally low performer willing to gamble, about 1% of the time
the NIS strategy can raise your reported measure .2 logits or more
- perhaps just enough to lift you above some crucial criterion
value. I understand that, in light of this, GRE procedures have
been modified.
Thomas O'Neill
American Society of Clinical Pathologists
2100 W. Harrison St.
Chicago IL 60612-3798
Slater SC, Schaeffer GA (1996) Computing scores for incomplete
GRE general computer adaptive tests. Paper presented at NCME, New
York.
Score inflation due to examinee control of a stopping rule. O'Neill T. … Rasch Measurement Transactions, 1996, 10:3 p. 522.