Theoretical Prediction of Test Items

The Lexile theory of readability measurement is attempting for reading comprehension what Newtonian mechanics achieved for astronomy. Initially, the Ptolemaic system of eccentric circles and epicycles described the motions of the planets more precisely than Newtonian mechanics. Newtonian mechanics, however, embodied a strong predictive theory which identified discrepancies for investigation and explanation. Explanations included telescope misalignment, the influence of unobserved planets (Uranus, Neptune), and short-comings in Newtonian theory (orbit of Mercury, since explained by Einsteinian relativity). The Ptolemaic system of making the model fit the data would have discovered none of these. Once established, however, Newtonian mechanics went far beyond astronomy, transforming physics and enabling our modern world.

Lexiles simplify the complex, content-ridden process of reading comprehension into two abstract, content-free components: syntactic load (quantified by sentence length) and semantic demand (quantified by word frequency). Even though reading experts insist that lexiles are a hopeless over-simplification, empirical work with Lexiles demonstrates that lexile theory-based item calibrations produce reading comprehension measures as accurate as any observational data-based calibration.

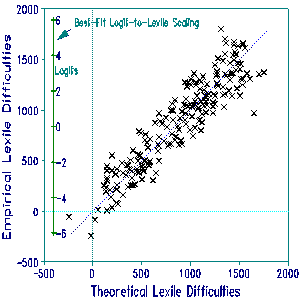
The Figure shows the relationship between lexile-theory and data-based calibrations for 200 sentence completion test items. The data-calibrations are in logits, rescaled to follow an identity line. In this relationship (which gives equal weight to theoretical and empirical values), the standard deviation of empirical values around the theoretical values is 177 lexiles (about 1 logit). Though departures from the identity line invite investigation, their impact on practical measurement with tests of reasonable length is negligible (see Wright & Panchapakesan, 1969).

Because of findings like this, several U.S. States are using lexiles as a fair and practical method for equating nationally published and locally produced reading comprehension tests.

Wright B.D. & Panchapakesan N. 1969. A procedure for sample-free item analysis. Educational and Psychological Measurement, 29, 23-48.

Theoretical prediction of test items. Burdick B, Stenner AJ. … Rasch Measurement Transactions, 1996, 10:1 p.475

Rasch Publications
Rasch Measurement Transactions (free, online)	Rasch Measurement research papers (free, online)	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Applying the Rasch Model 3rd. Ed., Bond & Fox	Best Test Design, Wright & Stone
Rating Scale Analysis, Wright & Masters	Introduction to Rasch Measurement, E. Smith & R. Smith	Introduction to Many-Facet Rasch Measurement, Thomas Eckes	Invariant Measurement: Using Rasch Models in the Social, Behavioral, and Health Sciences, George Engelhard, Jr.	Statistical Analyses for Language Testers, Rita Green
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Journal of Applied Measurement	Rasch models for measurement, David Andrich	Constructing Measures, Mark Wilson	Rasch Analysis in the Human Sciences, Boone, Stave, Yale
in Spanish:	Análisis de Rasch para todos, Agustín Tristán		Mediciones, Posicionamientos y Diagnósticos Competitivos, Juan Ramón Oreja Rodríguez

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt101b.htm

Website: www.rasch.org/rmt/contents.htm