"Diseño de mejores pruebas,
utilizando la Técnica de Rasch"

Gracias. Es un honor haber sido invitado a presentar aquí una Ponencia Magistral sobre el tema del "Diseño de mejores pruebas, utilizando la Técnica de Rasch". Como ya saben ustedes, éste es el título de un libro originalmente publicado por MESA Press de la Universidad de Chicago en mil nueve ciento setenta y nueve. La palabra MESA es la sigla en inglés de "medida, evaluación y análisis estadístico". El libro fue escrito por el Profesor Benjamin D. Wright, director del Laboratorio de Psicometría de MESA, y el Profesor Mark H. Stone, ahora Decano del Instituto de Psicología Adler en Chicago. En los años setenta, el Profesor Stone estaba en una situación muy parecida a la de muchos de ustedes. Trataba de medir áreas de funcionamiento mental que él mismo apenas entendía. Cuando conoció al Profesor Wright, pronto se persuadió de que la medida de Rasch era la llave que iba a abrir los pesados cerrojos y cadenas que parecían obstaculizar su propio progreso. A medida que trabajaban juntos, se dieron cuenta de que las dificultades encontradas por el Señor Stone eran las mismas que tenían muchos que se iniciaban en el campo. De manera que se escribió el libro.

Distinguished Visitors to "4 times heroic" Veracruz, attending III National Forum on Educational Evaluation, October 1998. From left to right: Antonio Gago Huguet, Director-general of CENEVAL; John Michael Linacre, Director, MESA Psychometric Laboratory; Rafael Vidal Uribe, Technical director, CENEVAL; Pedro Ramirez, University of Antioqua, Colombia; Javier Díaz de la Serna, Revisión Editorial, III Forum Proceedings, CENEVAL; Nazario Martínez Luján, Director, Escuela Preparatoria Federal por Cooperación El Chamizal, Chihuahua; Eduardo Backhoff Escudero, Autonomous University of Baja California

Yo he trabajado muy de cerca con ambos autores durante los últimos doce años, actualmente como Director Asociado del Laboratorio de Psicometría de MESA. El libro ha tenido una gran influencia en mi propia vida profesional. Me complace que ahora se haya traducido al español, bajo la dirección de Rafael Vidal, y que se me haya invitado para decir algunas palabras sobre el libro, así como sobre la filosofía que el mismo representa.

El progreso de la ciencia y de la tecnología no ha sido parejo a través de los siglos. En algunas áreas, ha habido pocos adelantos mientras que en otras se han producido grandes avances. Vivimos en una época de grandes adelantos. Los problemas que antes se consideraban insolubles ahora se resuelven de manera casi rutinaria. Nos hemos acostumbrado tanto a drásticos adelantos en la medicina, el transporte y la electrónica, que a veces no nos fijamos en el progreso más sutil, aunque igualmente impresionante, que se produce en otros campos.

La teoría de medición de Georg Rasch es un ejemplo del progreso en el que no nos fijamos. En primer lugar, resuelve un problema que generalmente no se considera como un problema en lo absoluto. Es el problema de las puntuaciones totales en pruebas, de las puntuaciones brutas. La solución de este problema abre las puertas a otros avances.

¿Por qué no se suele considerar como un problema la puntuación bruta en una prueba? Porque existe un acuerdo general de que una puntuación bruta más alta corresponde a un rendimiento en un nivel superior en la variable subyacente que está midiendo la prueba. La puntuación más alta merece el elogio y el premio. La censura y el castigo son el destino de la puntuación más baja. Un punto intermedio entre la puntuación más alta y la más baja es la puntuación que corresponde a un rendimiento mínimo satisfactorio. Esto suele ser todo lo que se requiere de las puntuaciones de las pruebas. De hecho, las puntuaciones brutas funcionan bastante bien, pero así funcionó la astronomía basada en los epiciclos de Ptolomeo de Alejandría.

¿Por qué es un problema la puntuación bruta en una prueba? Porque es ordinal, ambigua y específica de un contexto.

Antes de tratar estos problemas, permítanme atraer su atención de nuevo hacia el primer libro que los explicó de manera eficaz a los constructores y analistas de pruebas. Ese libro se titula "Diseño de mejores pruebas, utilizando la Técnica de Rasch", escrito por los Profesores Benjamin D. Wright y Mark H. Stone, ahora traducido al español por un equipo coordinado por Rafael Vidal, Director Técnico de CENEVAL.

Hace más de 100cien años, los estadísticos empezaron a notar imperfecciones en las propiedades numéricas de las puntuaciones de pruebas. En 1890, el Profesor Francis Ysidro Edgeworth observó que las calificaciones de ensayos exhibían amplias variaciones de tal manera que las calificaciones concedidas a cualquier tipo de rendimiento contenían un elemento considerable de azar. Esto causaba perplejidad en una época en que la física clásica parecía a punto de convertir al universo en una máquina completamente predecible. Por supuesto, ahora todos estamos familiarizados con el término de "mecánica cuántica". De hecho, el sorprendente éxito de esa teoría nos ha conducido a casi todos nosotros a abandonar la noción de un universo determinista. Pero el determinismo en las puntuaciones de pruebas está más enraizado. Muchos aún sienten, en lo más profundo de sí mismos, que "un 10 diez es un 10 diez".

Observen la primera diapositiva, Figura 1.2.1 en el libro. La línea horizontal describe el tema subyacente de la prueba. El extremo de la izquierda es el lado fácil, mientras que el extremo de la derecha es el lado difícil. Se muestran pruebas diferentes de ocho reactivos. En cada prueba, el reactivo más fácil tiene dificultad d1, y el más difícil tiene d8. La misma persona toma las ocho pruebas. En la prueba más fácil, obtiene una puntuación de ocho. En la prueba más difícil, obtiene cero. Y en las otras pruebas, es posible que obtenga cualquier puntuación intermedia. El significado de la puntuación bruta depende de su contexto.

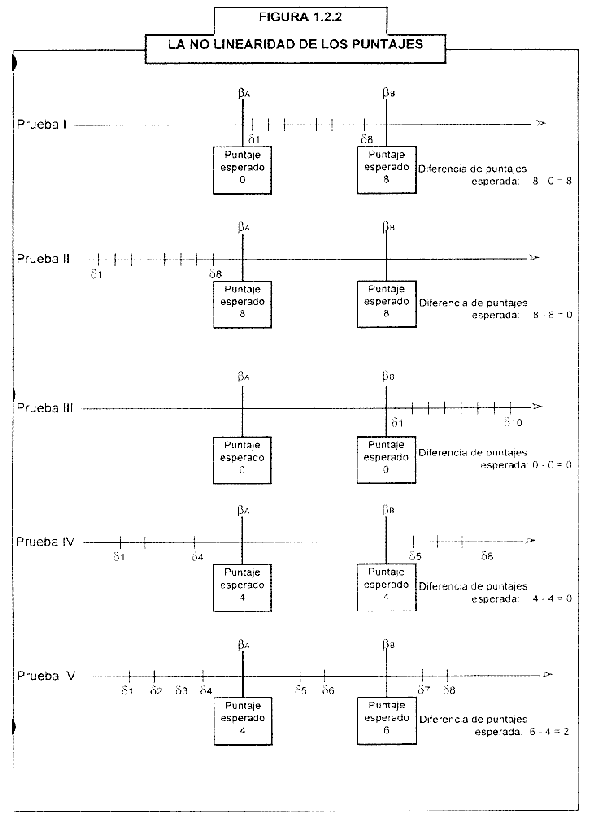
Ahora fíjense en la segunda diapositiva, Figura 1.2.2 en el libro. La naturaleza específica de contexto de las puntuaciones brutas se torna aún más problemática cuando se compara el rendimiento de dos personas, A y B. Podemos ver que si los reactivos de la prueba son muy difíciles para la persona A, entonces se espera que A obtenga cero de puntuación. Si los mismos reactivos de la prueba son fáciles para la persona B, entonces se espera que B obtenga una puntuación de ocho. Muestran la diferencia máxima de puntuación bruta. ¡Qué distintos son! Pero si se administra una prueba mucho más fácil, entonces se espera que tanto A como B obtengan ocho. ¡Qué parecidos son!

¿Cómo puede ocurrir esto? Esto ocurre debido a que la puntuación bruta es una medida de intervalos ordinal, no lineal. Estamos tan acostumbrados a las medidas lineales como los metros y gramos, que tendemos a pensar que todas las cantidades numéricas son medidas lineales. Pero sabemos que no es así. Por ejemplo, la escala Richter para temblores de tierra no es una escala lineal.

¿Qué significa el término "escala lineal"? Significa que "una unidad más" en la escala es la misma cantidad adicional donde sea que ocurra en la escala. Esto es cierto para gramos y metros. Un gramo más que se añade a un gramo es la misma cantidad adicional que un gramo más que se añade a un kilogramo. Para la escala de Richter, "una unidad más" no tiene un significado constante. La diferencia entre cinco y seis es diez veces superior a la que existe entre cuatro y cinco.

Para las puntuaciones brutas, el valor de "una unidad más" causa aún más perplejidad. En primer lugar, no existe el concepto de "una unidad más" más allá de la máxima puntuación de una prueba. Las puntuaciones de pruebas tienen un rango restringido. Pero el área del tema o la variable subyacente que representan no tienen tal restricción. Siempre nos podemos imaginar un reactivo más difícil que cualquiera de los que se hayan presentado, o una persona más hábil que cualquiera de las que se hayan encontrado.

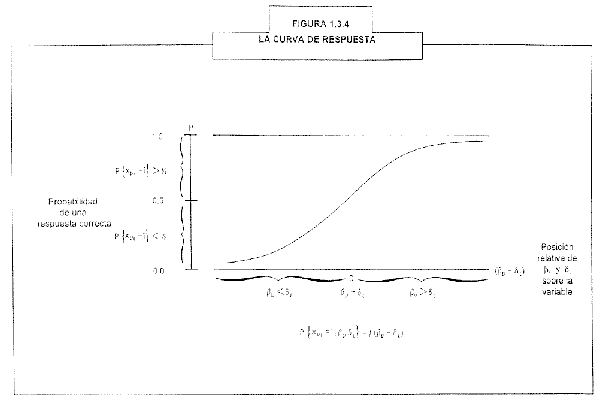
En la tercera diapositiva aparece la relación entre una puntuación restringida y una variable subyacente no restringida , Figura 1.3.4 en el libro. El eje horizontal describe el rendimiento en el área del tema que va desde un rendimiento muy pobre en el lado izquierdo hasta un rendimiento muy alto a la derecha. De hecho, esta línea es infinitamente larga. Esta diapositiva sólo muestra la parte central. La línea es la escala de medida lineal que queremos.

El eje vertical corresponde a la puntuación bruta que observamos. En esta diapositiva, nos hemos concentrado en el rendimiento esperado en un reactivo específico de la prueba. El reactivo está ubicado en el punto di. ¿Qué esperamos? ¿Que los examinados pasen o que fallen en este punto? Por lo general, esperamos que fallen los examinados con menos habilidad de lo que tiene el reactivo de difícil. Esperamos que pasen los examinados con más habilidad de lo que tiene el reactivo de difícil. En 1947, el psicometrista Louis Guttman decía que las personas más hábiles deben pasar los reactivos más fáciles. Pero ésta es una visión determinista del universo. En 1925, Louis Thurstone se dio cuenta de que existe un elemento de azar en todos los rendimientos. Lo único que podemos decir es que las personas más hábiles tienen más probabilidades de pasar que las personas menos hábiles, no que deben pasar. Por consiguiente, el eje vertical en la diapositiva se muestra como la probabilidad de éxito en el reactivo, que va desde cero, sin éxito, a uno, éxito completo. Para una persona exactamente a la par del reactivo, podemos predecir ni éxito ni fracaso, de manera que la probabilidad de éxito es de punto cinco (0.5).

La relación entre las puntuaciones brutas y las medidas es compleja aun para el caso más simple, el de un solo reactivo. Sin embargo, vemos que esta relación tiene la forma de una ojiva. ¿Cuál es la expresión matemática para esta ojiva? Si tratamos de construirla a partir de datos, obtenemos la curva característica del reactivo observado. Pero esto se aplica a una prueba específica y a una selección de personas. Contiene todos los golpes y accidentes de la vida real.

La medida en intervalo es un ideal. Una regla métrica o un termómetro por necesidad tienen imperfecciones. Ignoramos estas imperfecciones tanto en la manera en que se fabricó el instrumento como en la manera en que se utiliza. Por ejemplo, idealizamos una distancia de seis metros, de tal manera que ya no nos preocupa quién hizo la medida o qué instrumento de medición se utilizó.

En la construcción de una prueba, esto se llama la curva característica del reactivo "modelo". Es una ojiva, pero ¿con qué forma? En 1925, Louis Thurstone pensó que debía relacionarse con la distribución normal y por tanto usó la ojiva acumulativa normal. Esto casi funciona. Pero aquí tenemos uno de los grandes adelantos en la obra de Georg Rasch.

En 1953, se le pidió al matemático danés Georg Rasch que analizara algunas pruebas de inteligencia. Después de cierta investigación matemática, percibió que la forma ideal para la curva característica es la ojiva log_eística. Esta forma es la única que permite estimar la habilidad de una persona independientemente del reactivo en particular en la prueba. También es la única que permite estimar la dificultad de un reactivo independientemente del grupo de personas que tomaron la prueba. Convierte las puntuaciones brutas ordinales en medidas lineales.

(Probabilidad de Éxitor) El Logaritmo --------------------------- (Probabilidad de Fallo)

= la Habilidad del la Persona   - La Dificultad del Reactivo

Observen la cuarta diapositiva. Para los que se inclinan hacia las matemáticas, aquí tenemos el modelo de Rasch. El logaritmo de la Probabilidad de Éxito dividido entre la Probabilidad de Fallo es igual a la Habilidad de la Persona menos la Dificultad del Reactivo. Estas probabilidades deben ser estimadas a partir de los datos; pero no se preocupen por las complejidades matemáticas del proceso de estimación. ¡Para eso están las computadoras!

Este modelo tiene la misma relación con la construcción de pruebas que la Ley del Movimiento de Newton tiene para la física. Mientras mejor entienda el diseñador de una máquina a la Ley del Movimiento, mejor será su máquina. Mientras mejor entienda el constructor de pruebas al modelo de Rasch, mejor será la prueba.

¿Pero cómo va el constructor de pruebas a entender e implementar el modelo de Rasch? Aquí radica el gran adelanto producido por el libro "Diseño de mejores pruebas".

Antes de la primera publicación de este libro en 1979, se publicaron artículos en revistas. Existía el propio libro de Georg Rasch: "Modelos probabilísticos para algunas pruebas de inteligencia y de logros". Hubo otros libros también, pero o eran demasiado matemáticos o se limitaban a estrechas aplicaciones del modelo de Rasch. El libro "Diseño de mejores pruebas", permitió que la utilización eficaz del modelo de Rasch estuviera al alcance de todos.

Existe otro importante aspecto de las puntuaciones brutas que es preciso considerar aquí: su ambigüedad. Observen la quinta diapositiva, extracto de la Tabla 3.2.1 del libro. Muestra las respuestas de varias personas ante una prueba. Todas estas personas obtuvieron la misma puntuación bruta. Pero la obtuvieron de diferentes maneras. ¿Qué representan estas diferencias?

Cuando pensamos en una puntuación bruta de 7 de 14, esperamos que la persona pase los siete reactivos más fáciles y falle en los siete más difíciles. Así fue cómo se desempeñó la primera persona en esta diapositiva. Esto es lo que sugiere el sentido común. Esto es lo que predice el modelo Rasch. Esto fue lo que afirmó Louis Guttman. Pero no siempre ocurre así. De hecho, en pruebas largas, es raro que ocurra.

Para la segunda persona en la diapositiva, sólo existe una pequeña desviación de nuestra expectativa. Es probable que ignoremos esta discrepancia y la consideremos como una indicación de que ciertamente vivimos en un mundo estructurado por "el tiempo y el azar".

Para la tercera persona, tenemos un dilema. Hay ambigüedad en la serie de respuestas y ambigüedad en la medida resultante. ¿Actuamos de acuerdo al éxito de esta persona en un reactivo difícil y la declaramos un genio? ¿O actuamos de acuerdo al fallo de esta persona en un reactivo fácil y la declaramos idiota? Obviamente ambas acciones son muy extremas. Desde la perspectiva de la medida, el éxito imprevisto y el fallo imprevisto se anulan mutuamente, de manera que todas las maneras de realizar la misma puntuación bruta en los mismos reactivos estiman la misma medida. Pero no siempre con la misma exactitud.

El modelo de Rasch predice cierto nivel de imprevisión en el patrón de respuesta, así como el Principio de Incertidumbre de Heisenberg limita la exactitud de la medida física. El modelo de Rasch también señala cuándo se excede ese nivel de incertidumbre y causa que se degrade la exactitud de la medida. Ya no estamos seguros de lo que significa una puntuación bruta, de manera que ya no podemos obtener una medida exacta. Esto ocurrió con la tercera persona.

¿Qué pasa si cada respuesta es exactamente como lo predice el modelo de Rasch? Entonces tenemos una paradoja. El modelo de Rasch predice no sólo las respuestas en sí, sino también el nivel de incertidumbre asociado con ellas. Para la primera persona en la diapositiva, cada respuesta es exactamente lo que predice el modelo de Rasch. No hay imprevistos ni incertidumbre. Pero esto contradice otra predicción del modelo de Rasch. Esta predicción es que existe cierto nivel de imprevisión en las respuestas.

¿Cuál es la implicación de no tener incertidumbre? Luego sospechamos que existe algún otro factor que está constriñendo las respuestas de la persona. Por ejemplo, ésta puede ser una prueba con un límite de tiempo. La primera persona trabaja con lentitud y cuidado en estos reactivos, que han sido ordenados de fáciles a difíciles. La persona responde correctamente a cada reactivo. Pero se acaba el tiempo. La persona sólo ha llegado a la mitad de la prueba. Esto produce la primera serie de respuestas. ¿Acaso creemos que esta serie de respuestas representa con exactitud la habilidad de la persona? No, es claro que la persona puede pasar los reactivos más difíciles. La medida para la primera persona es ambigua. Dice: "éste es el nivel de rendimiento de la persona bajo estas condiciones de la prueba", pero también dice: "no espere este nivel de rendimiento bajo otras condiciones". Sin embargo, la razón por la que dimos la prueba fue la de generalizar el rendimiento a otras condiciones más allá de la prueba.

El modelo de Rasch no puede resolver el problema de la ambigüedad, pero puede indicar dónde y hasta qué punto hay ambigüedad. Nos puede ayudar a diseñar pruebas menos susceptibles de producir resultados ambiguos. Nos puede ayudar a producir medidas más exactas, aplicables a una gama más amplia de situaciones distintas.

Consideremos ahora varios aspectos sustanciales y prácticos relacionados con la medida de Rasch y que se explican en el libro "Diseño de mejores pruebas".

Nos hemos referido a los reactivos como "fáciles" y "difíciles". Así es cómo se ven desde el punto de vista de las personas que toman la prueba. Pero estos reactivos existen con la intención de representar alguna área de contenido, una construcción teórica o una variable psicológica. Un reactivo fácil debería representar un nivel inferior, más elemental o una primera fase de una variable. Un reactivo difícil debería representar un nivel superior, más avanzado o una última fase de una variable. ¿Pero es así?

La construcción de medidas lineales de la dificultad de un reactivo significa que los reactivos pueden colocarse en línea según su dificultad. Esta línea tiene las mismas propiedades que esperamos observar cuando observamos una regla métrica. Las distancias iguales implican diferencias iguales.

Observen la sexta diapositiva. Aquí tenemos una muestra de algunos de los reactivos de la Prueba de Cubo Knox, la cual se discute en este libro. Los números indican el patrón que el examinado debe memorizar y repetir ante el examinador. Algunos patrones son fáciles de recordar. Éstos aparecen en la parte de abajo. Algunos son difíciles de recordar. Éstos aparecen en la parte de arriba. Para su referencia, a la izquierda se muestra la distribución de una muestra de personas que tomaron la prueba. Esta diapositiva fue producida a partir de los resultados del programa de computadora, WinSteps, utilizando los datos publicados en el libro. WinSteps es una implementación actual de la metodología Rasch, basada en la teoría que se plantea en el libro. WinSteps es el resultado de otros veinte años de aplicación de las técnicas de medición de Rasch por miles de constructores y analistas de pruebas de todo el mundo.

La diapositiva es muy instructiva. Observen que existe un vacío en medio de los reactivos. Este vacío se alinea con la ubicación de la mayoría de las personas. En esta prueba, la mayoría de nuestros seleccionados encontró que los reactivos eran fáciles o difíciles. Hubo pocos reactivos precisos. Podemos mejorar esta prueba mediante el diseño de nuevos reactivos para llenar el vacío. ¿Pero cómo se verán estos reactivos?

A medida que observamos de arriba abajo la jerarquía de reactivos, pronto vemos lo que hace que estas pruebas sean fáciles o difíciles. Mientras más dígitos hay, más difíciles son los reactivos. Mientras más inversiones de secuencias, como 1-3-2, más difíciles son los reactivos. Este tipo de información puede inferirse fácilmente a partir del mapa de reactivos que aparece en la diapositiva. Ahora podemos diseñar reactivos para llenar el vacío. Uno de estos reactivos es 3-1-4-2. Tiene cuatro dígitos, por lo que debería ser más fácil que el reactivo de cinco dígitos, 1-3-1-2-4. Tiene dos inversiones, por lo que debería ser más difícil que 2-4-3-1, el cual sólo tiene una inversión.

Observen la séptima diapositiva. Después de administrar este reactivo a nuestros seleccionados, ¡descubrimos que el nuevo reactivo llena el vacío!

Al usar el modelo de Rasch, obtuvimos un útil mapa de la variable. Después descubrimos una imperfección en la prueba. Luego pudimos construir una teoría sobre qué hace que los reactivos sean difíciles. Después pudimos escribir un nuevo reactivo. Y finalmente pudimos verificar que el reactivo corregía la imperfección de la prueba. ¡Es de esta manera que la ciencia y el conocimiento progresan! Hemos dividido el átomo.

Por supuesto, de la misma manera que descubrimos nuevas verdades sobre la prueba y los reactivos, también podemos diagnosticar el rendimiento de los que toman la prueba. ¿Nos interesan las diferencias en los estilos de aprendizaje de las niñas y de los niños? ¡El modelo de Rasch puede servir! ¿Nos interesa comparar los rendimientos entre escuelas o entre años escolares? ¡El modelo de Rasch puede servir!

Un severo desafío para la medición es el que provocó por primera vez el interés de Georg Rasch en la medida educativa. ¿Cómo se compara el rendimiento en dos pruebas diferentes de la misma área de contenido? Al principio este problema parece ser trivial. Simplemente compare las puntuaciones brutas. Pero quizás una prueba es más difícil que la otra. Quizás una prueba abarca una gama más amplia de rendimiento que la otra. Quizás una prueba es administrada a estudiantes con más habilidad que otros. Ahora, es posible que las puntuaciones no se puedan comparar. De hecho, éste suele ser el caso. Luego el problema de la comparación parece no tener solución: existen demasiados factores desconocidos que deben identificarse y compararse. Por supuesto, bajo condiciones muy controladas, se pueden indagar las equivalencias entre las pruebas. Pero ¿cómo podemos verificar que los controles funcionaron?

La medida de Rasch proporciona una solución tan fácil para este problema que muchos analistas la rechazan porque dicen que es demasiado simple. Y, sin embargo, estos mismos analistas aceptan esta solución sin cuestionamiento cuando comparan sus propios pesos tal como aparecen en diferentes básculas caseras. Tal como lo explica nuestro libro con minuciosos detalles, la solución es construir dos mapas de reactivos, uno para cada prueba.

Observen la séptima diapositiva. Los dos mapas son nuestrôs dos básculas caseras. Están colocados uno al lado del otro. Luego utilicen algún método práctico para conectarlos o alinearlos. Por ejemplo, si un examinado ha tomado ambas pruebas, ese examinado debería estar en el mismo lugar en ambos mapas. Si se incluye el mismo reactivo en ambas pruebas, ese reactivo debería estar en el mismo lugar en ambos mapas. Si los reactivos se refieren a un material de la misma complejidad, como una suma de dos dígitos, entonces estos reactivos deberían estar en el mismo lugar en ambos mapas. La combinación de estos métodos permite que el analista verifique la equivalencia de las pruebas para asegurarse de que las idiosincrasias asociadas con una u otra prueba no intervengan en los resultados.

El modelo de Rasch estimula la igualdad y apertura en la construcción, el análisis y el informe de las pruebas. Podemos mostrarlo todo en los diagramas. Observen la octava diapositiva. Esto ya se hizo en Australia. A cada padre se le da un mapa que muestra el rendimiento de su hijo. No hay dudas ni disputas sobre el área en que el niño o la niña ha tenido éxito o ha fallado. No hay duda sobre lo que puede hacer el niño o la niña. No hay duda sobre dónde ha tenido éxito más allá de las expectativas. No hay duda sobre dónde se ha quedado atrás. No hay duda sobre lo que hay que enseñarle después.

En todas las áreas de la ciencia, una mejor medición ha originado una mejor teoría y por tanto, una mejor práctica. Ésta es exactamente la misma situación con la medida de Rasch.

En conclusión, me gustaría transmitirles a ustedes el profundo aprecio de los autores de "Diseño de mejores pruebas", Ben Wright y Mark Stone. Se sienten honrados de que CENEVAL haya traducido su libro y me han pedido que presente esta copia firmada a Rafael Vidal. Permítanme leerles sus dedicatorias:

Del Profesor Mark Stone:
"A Rafael, con mis mejores deseos y mi agradecimiento por sus esfuerzos."

Del Profesor Ben Wright:
"A mi querido amigo y colega Rafael, quien hizo posible esta traducción y permitió que se completara, con mi eterno agradecimiento."

Gracias por su atención, damas y caballeros.

Ponencia Magistral de III Foro Nacional de Evaluación Educativa,
29 de octubre de 1998, H. Veracruz, V., México,
de John Michael Linacre. MESA Memo # 68. 1998.

Translated by www.transperfect.com.

Diseño óptimo de pruebas [Spanish Translation of Best Test Design] by Benjamin D. Wright & Mark H. Stone, translation by A. Tristán-López & M.-M. Sánchez-Sifer, 2018. descargar
Para el lector poco familiarizado con el análisis de ítemes es una fortuna que Benjamín Wright y Mark H. Stone hayan escrito un libro fácilmente comprensible y que lleva de la mano al lector para entender la filosofía y la técnica del análisis de Rasch con ejemplos sencillos que dejan ver toda la potencialidad de la técnica.

Go to Top of Page
Go to Institute for Objective Measurement Page