Model selection: Rating Scale Model (RSM) or Partial Credit Model (PCM)?

In Rasch measurement, we construct data to fit the measurement model. On occasion, however, we have a choice of parameterization, most commonly between "rating scale" and "partial credit" parameters. The rating scale model specifies that a set of items share the same rating scale structure. It originates in attitude surveys where the respondent is presented the same response choices for several items. The partial credit model specifies that each item has its own rating scale structure. It derives from multiple-choice tests where responses that are incorrect, but indicate some knowledge, are given partial credit towards a correct response. The amount of partial correctness varies across items.

Statistically, removing an item from a rating scale grouping and allowing it to define its own partial credit scale introduces (number of categories - 2) extra parameters into the estimation. In general, more parameters mean a better fit of the data to the model. If misfit is reduced, then measurement appears to be better. So why not always use the partial credit model?

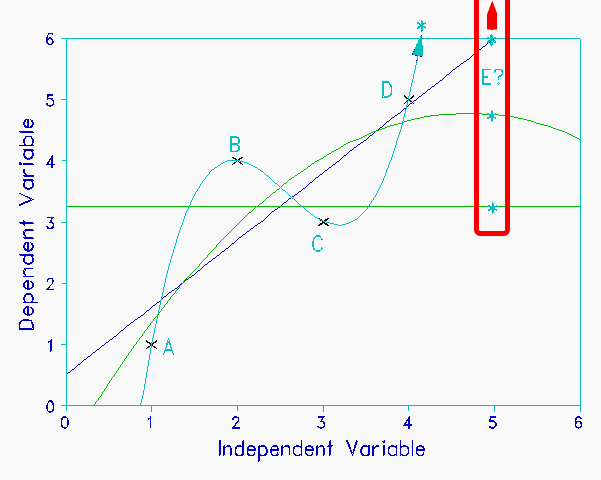
Figure 1 illustrates adding more parameters to a regression model. We have four points A, B, C, D. They are modeled with 4 lines: a constant, a linear regression, a quadratic and a cubic. The more complex the model, the better the fit between the model and the points. With the cubic it is perfect. We have optimized the fit of the model to these data. But what about new data? Say our purpose is to infer the y-value for point E, with x-value, 5. We now have 4 predictions. The constant yields 3.25; the linear model, 6; the quadratic, 4.75; and the cubic 17.04. By inspection, a value around 5 looks reasonable. 17, the value predicted by the model with perfect fit to these data, looks unreasonable. Better fit does not necessarily produce better inference. The scientific rule is Ockham's Razor: "What can be accounted for by fewer assumptions is explained in vain by more."

Various statistical tests have been devised to assist the analyst in model selection, but these are always advisory, never mandatory. Ultimately it is the meaning of the measures that motivates the choice of model. Consider an attitude survey of 30 items, each presented to the respondents with the same 4 category agreement scale: "Strongly disagree, Disagree, Agree, Strongly agree." When measures are communicated to others, it is impractical and mentally overwhelming to present a different rating scale structure for each item. Perhaps the audience can comprehend two structures, one for positively worded items and one for negatively worded items. Perhaps the responses to some items are essential "yes/no" and can be recoded as such. But, overall, for the results to be intelligible, the item hierarchy must be disentangled from the minutia of the rating scales.

Removing an item from a rating scale cluster and allowing it to define its own partial credit scale is not only expensive in terms of communication, but also limiting in terms of inference. Each item on a survey or questionnaire represents a universe of other similar items that could have been asked. As we think of these other items, do we place them in the rating scale cluster? Do we impute a particular item's partial credit scale to them? Or do we imagine each of these other possible items to have their own partial credit scales? We are at a loss. But if the original items are modeled to share a rating scale, then we feel secure in imputing that same scale to similar unasked items.

For items or subsets of items to be given their own scales, there needs to be strong evidence, statistically and substantively, that these particularized scales lead to different measures with different implications. Otherwise it is "a distinction without a difference" (Henry Fielding, 1749, Tom Jones, 6:13).

Benjamin D. Wright

See also Comparing and Choosing between "Partial Credit Models" (PCM) and "Rating Scale Models" (RSM), RMT, 2000, 14:3 p.768.

Model selection: Rating Scale Model (RSM) or Partial Credit Model (PCM)? Wright B.D. … Rasch Measurement Transactions, 1998, 12:3 p. 641-2.

Rasch Books and Publications
Invariant Measurement: Using Rasch Models in the Social, Behavioral, and Health Sciences, 2nd Edn. George Engelhard, Jr. & Jue Wang	Applying the Rasch Model (Winsteps, Facets) 4th Ed., Bond, Yan, Heene	Advances in Rasch Analyses in the Human Sciences (Winsteps, Facets) 1st Ed., Boone, Staver	Advances in Applications of Rasch Measurement in Science Education, X. Liu & W. J. Boone	Rasch Analysis in the Human Sciences (Winsteps) Boone, Staver, Yale
Introduction to Many-Facet Rasch Measurement (Facets), Thomas Eckes	Statistical Analyses for Language Testers (Facets), Rita Green	Invariant Measurement with Raters and Rating Scales: Rasch Models for Rater-Mediated Assessments (Facets), George Engelhard, Jr. & Stefanie Wind	Aplicação do Modelo de Rasch (Português), de Bond, Trevor G., Fox, Christine M	Appliquer le modèle de Rasch: Défis et pistes de solution (Winsteps) E. Dionne, S. Béland
Exploring Rating Scale Functioning for Survey Research (R, Facets), Stefanie Wind	Rasch Measurement: Applications, Khine	Winsteps Tutorials - free Facets Tutorials - free	Many-Facet Rasch Measurement (Facets) - free, J.M. Linacre	Fairness, Justice and Language Assessment (Winsteps, Facets), McNamara, Knoch, Fan
Other Rasch-Related Resources: Rasch Measurement YouTube Channel
Rasch Measurement Transactions & Rasch Measurement research papers - free	An Introduction to the Rasch Model with Examples in R (eRm, etc.), Debelak, Strobl, Zeigenfuse	Rasch Measurement Theory Analysis in R, Wind, Hua	Applying the Rasch Model in Social Sciences Using R, Lamprianou	El modelo métrico de Rasch: Fundamentación, implementación e interpretación de la medida en ciencias sociales (Spanish Edition), Manuel González-Montesinos M.
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Rasch Models for Measurement, David Andrich	Constructing Measures, Mark Wilson	Best Test Design - free, Wright & Stone Rating Scale Analysis - free, Wright & Masters
Virtual Standard Setting: Setting Cut Scores, Charalambos Kollias	Diseño de Mejores Pruebas - free, Spanish Best Test Design	A Course in Rasch Measurement Theory, Andrich, Marais	Rasch Models in Health, Christensen, Kreiner, Mesba	Multivariate and Mixture Distribution Rasch Models, von Davier, Carstensen

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt1231.htm

Website: www.rasch.org/rmt/contents.htm