Diagnosing Measure Covariance
Careful measurement is aimed at ascertaining the extent or
quantity of one particular attribute of something. In practice,
this ideal of unidimensional measurement is never achieved. It
proves impossible to isolate entirely one attribute from another,
e.g., length of steel rods and temperature, or time and very high
velocities. In the social sciences, measurement of unintentional
combinations of attributes is frequently encountered. This can
mislead the unwary into supposing that two different things are the
same.
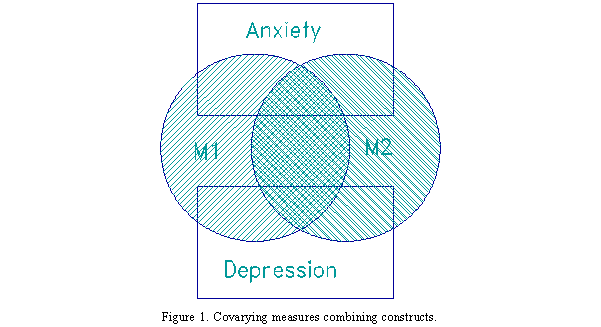Figure 1 illustrates a situation in which Measure 1 is intended to
quantify one attribute and Measure 2 another. Henry& Alred
(1996) encountered similar situations during their investigation of
Depression and Anxiety. Measure 1 was intended to measure anxiety,
but included some depression-sensitive items. Measure 2 was
intended to measure depression, but included some anxiety-influenced
items. Thus Measure 1 covaried with Measure 2 because both quantify
combinations of the two attributes. Usually combinations of two
different attributes are noticed because item misfit statistics can
classify the items according to their predominant attribute. Also,
calibrating the items with samples with different proportions of the
two attributes causes obvious shifts in the calibrations.
Suppose, however, that the two attributes have been clearly
defined and each measure quantifies only its intended attribute.
What if unidimensionality has been achieved, and yet the now
clearly unidimensional measures still covary? Can this happen?
Unidimensionality does not mean "one dimension totally unlike any
other". Rather, unidimensionality means one dimension comprising
more or less of the same one quality, however it is defined.
This quality may be closely related to other qualities. Height and
weight are usually considered distinct qualities, and measured as
such, but tall adults are generally heavier than short adults, so
that measures of height and weight will covary. Thus measures may
covary because the underlying qualities being measured overlap.
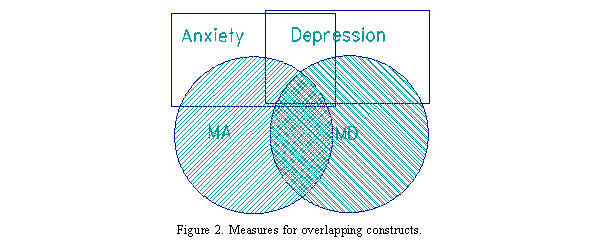Look again at depression and anxiety. These are commonly observed
to occur together and may well be manifestations of some more basic
psychological state. Their relationship may be that depicted in
Figure 2. Measure A focuses sharply on Anxiety, and Measure D
focuses sharply on Depression. Both measures are unidimensional,
but because the circumstances causing manifestation of the two
attributes overlap, the measures covary.
When measures are discovered to covary across attributes, the
test developer faces the challenge of constructing items that probe
the desired attribute at a more demanding level than its companion
attribute. For arithmetic word problems, the arithmetic task must be
markedly more demanding than the reading comprehension task. But
this requires care. Give arithmetic word problems written in
English to a French speaker, and the test no longer measures
arithmetic, but rather ESL proficiency.
Based on Henry D. & Alred K. (1996) Measuring Depression in
Children with Achenbach's Checklist. MOMS, December 1996.
Diagnosing Measure Covariance. Henry D., Alred K. … Rasch Measurement Transactions, 1997, 11:1 p. 556